Reed frogs

Reed frogs Survival Analysis

  density pred  size surv propsurv
1      10   no   big    9      0.9
2      10   no   big   10      1.0
3      10   no   big    7      0.7
4      10   no   big   10      1.0
5      10   no small    9      0.9
6      10   no small    9      0.9

But those QQ plots…

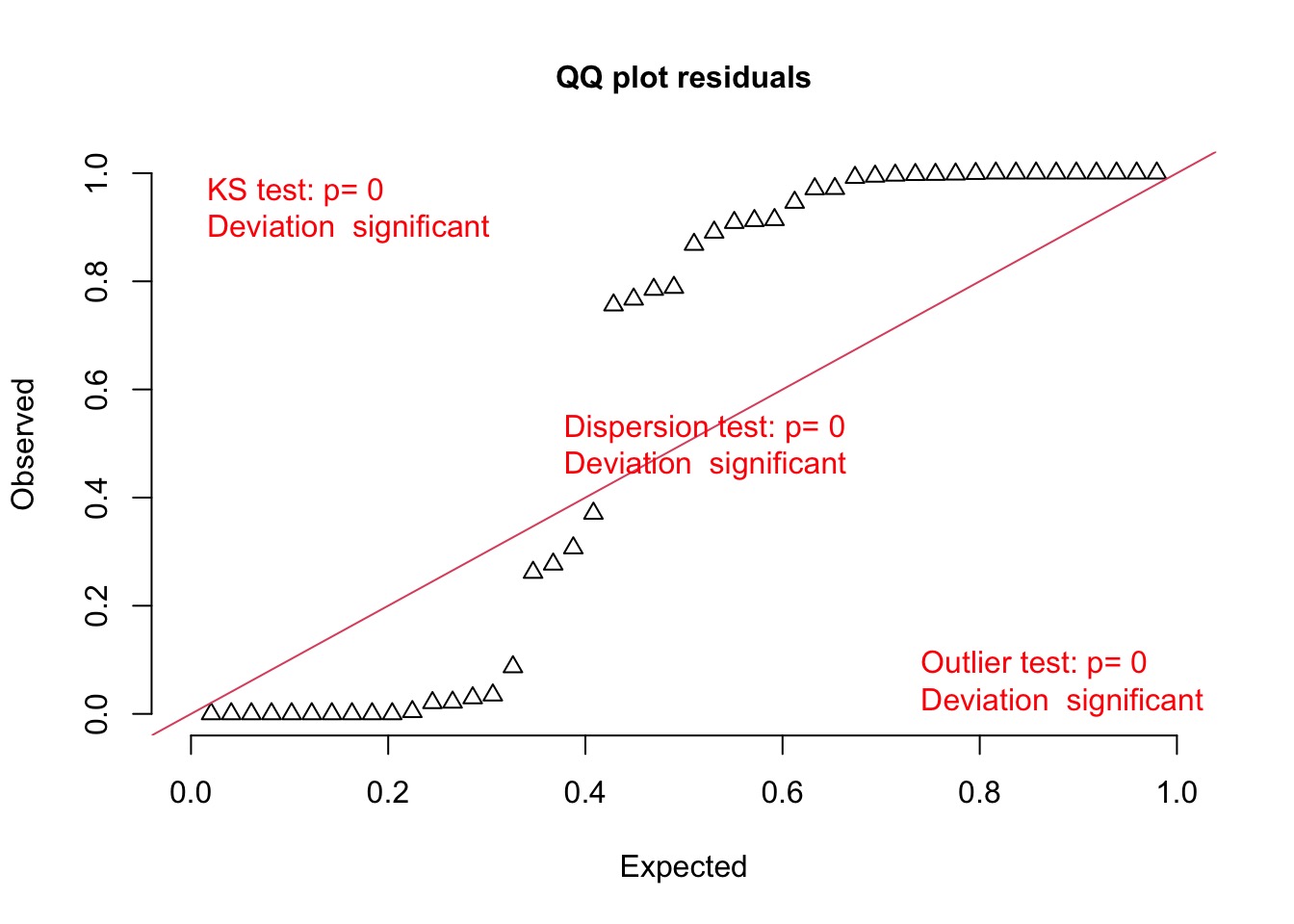
What is Overdispersion

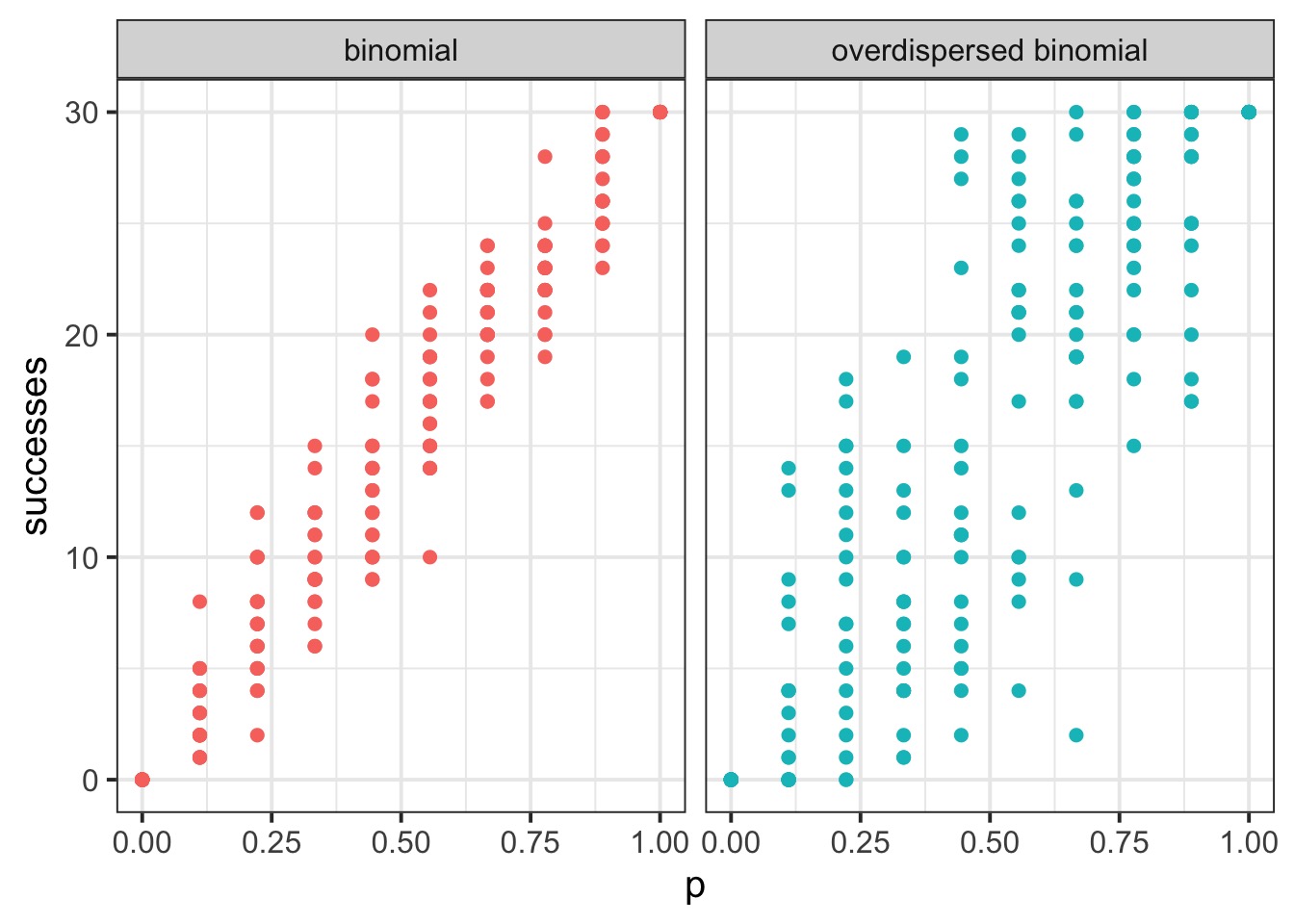
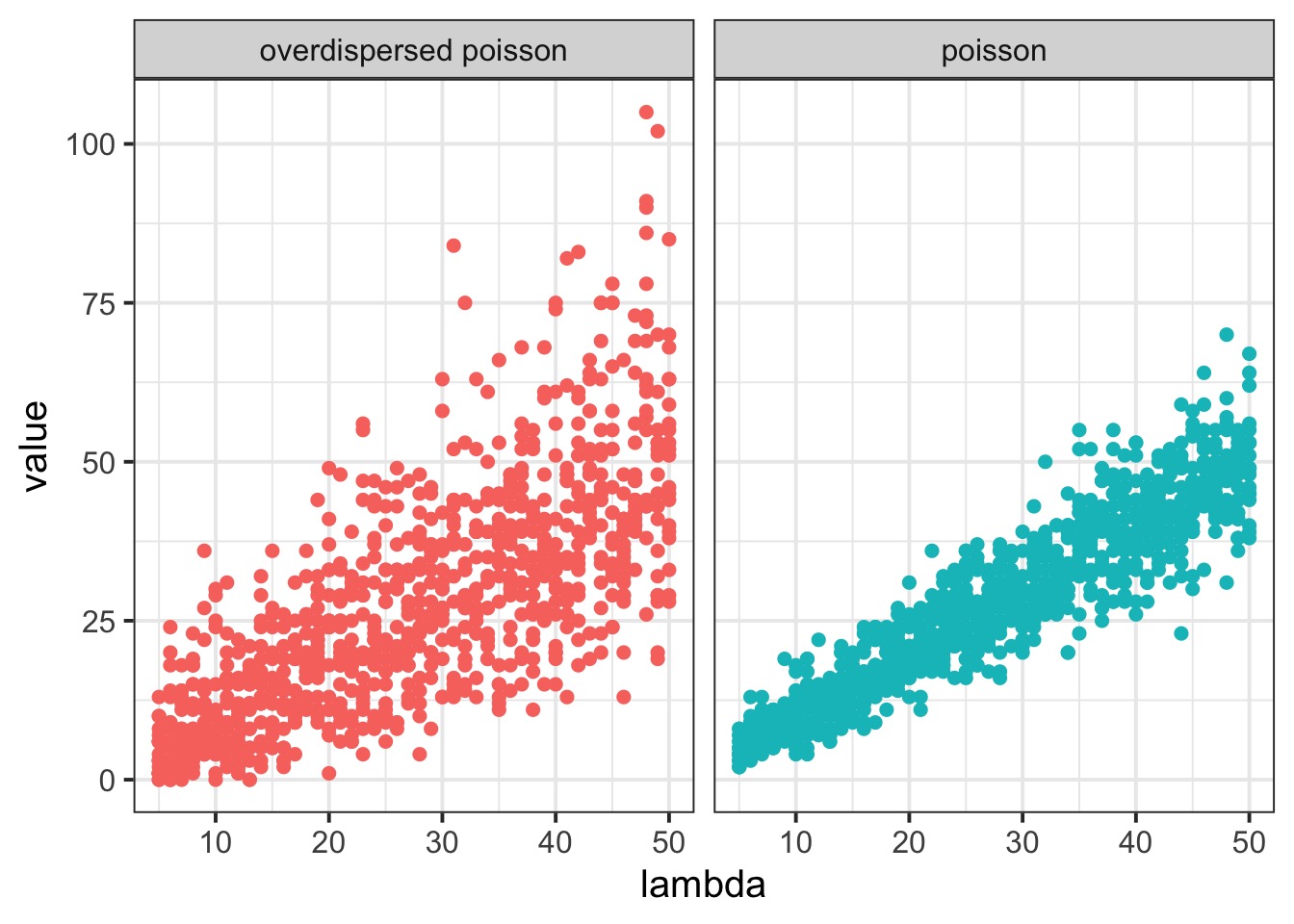
• We expect Binomial, Poisson, and other relationships to have a fixed relationship with their variance.
  - For Poisson, variance = mean. - For Binomial, the variance is size*p(1-p).

• Overdispersion is when we use these distributions, but fail to meet the above assumption.

Overdispersed Binomial

Overdispersed Poisson

What could over/underdispersion indicate?

1. We are missing key predictors

2. We are failing to model heterogeneity in predictions due to autocorrelaiton

   • Random Effects
     
   • Temporal autocorrelation
     
   • Spatial autocorrelation

3. We are using the wrong error distribution

Mixture-based solutions

• We can mix distributions in two ways

• First, we can apply a scaling correction - a Quasi-distribution

• OR, we can mix together two distributions into one!

Quasi-distributions and a Scaling Parameter

Binomial pdf: \[P(X=k)={n \choose k}p^{k}(1-p)^{n-k}\]

Quasi-binomial pdf: \[P(X=k)={n \choose k}p(p+k\phi)^{k-1}(1-p-k\phi)^{n-k}\]

Some Quasi-Information

• Parameter estimates unaffected (same estimate of mean trend)

• SE might change

• Uses ‘quasi-likelihood’

• We need to use QAIC instead of AIC to account for overdispersion

• Really, we fit a model, then futz with \(\phi\) to accomodate error

Let’s Cook with Flame: Pure Mixture Distributions

Consider…
    \(X \sim Bin(n,p)\)

    \(p\sim Beta(\alpha,\beta)\)

with \(\alpha = p \theta\) and \(\beta = (1-p) \theta\)

or

    \(p\sim BetaBin(n, \hat{p},\theta)\)

The Beta

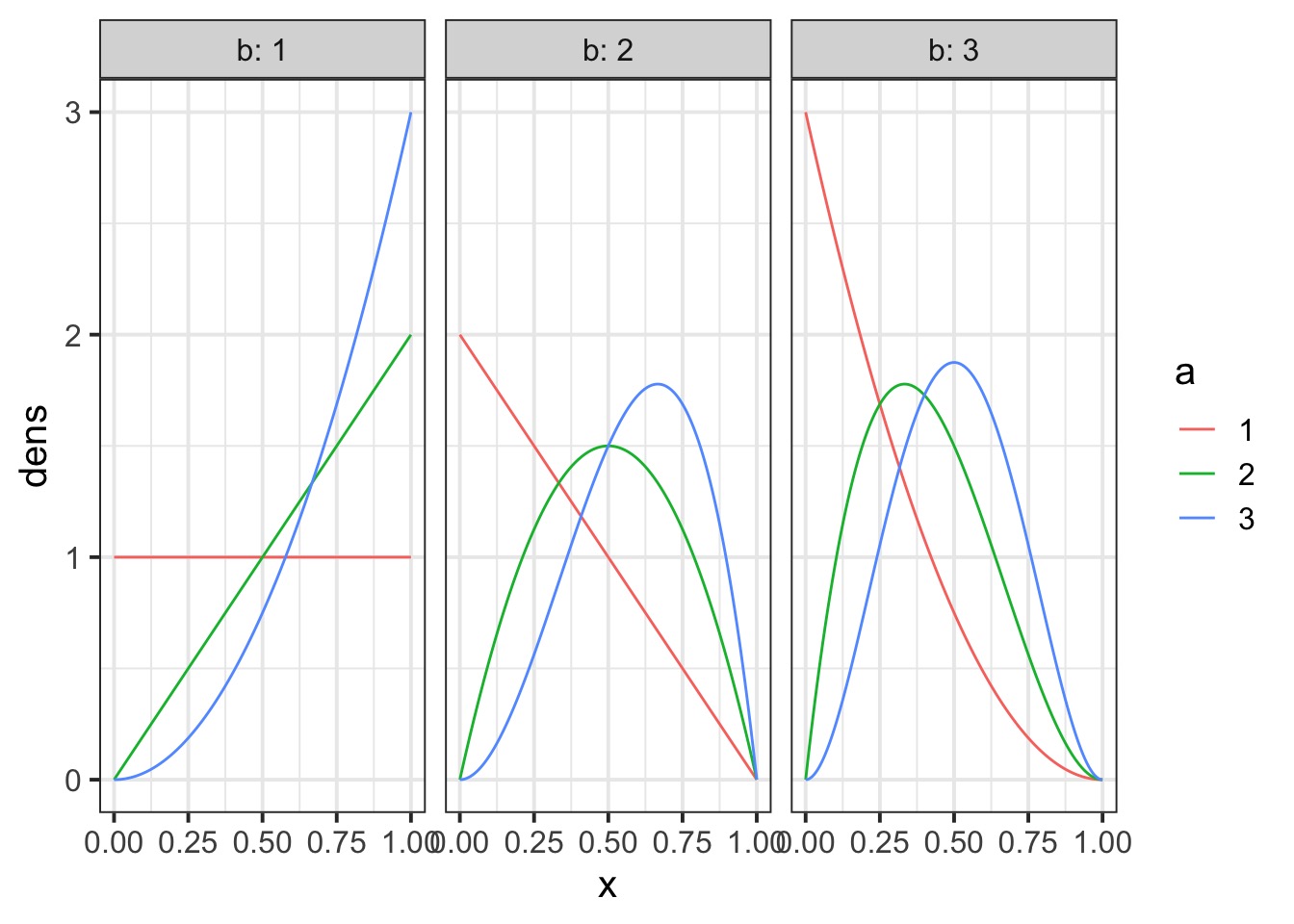
How does the beta binomial change things?

How does the beta binomial change things?

How does the beta binomial change things?

How does the beta binomial change things?

A Bayesian Approach

reedfrogs$d <- scale(reedfrogs$density)

reed_bb_mod <- alist(
  # likelihood
  surv ~ dbetabinom(density, prob, theta),
  
  # DGP
  logit(prob) <- a + b*d,
  
  # priors
  a ~ dnorm(0,2),
  b ~ dnorm(0,2),
  theta ~ dexp(1)
)

reed_bb_fit <- quap(reed_bb_mod, data=reedfrogs)

An Exponential Prior?

Or An Cauchy Prior?

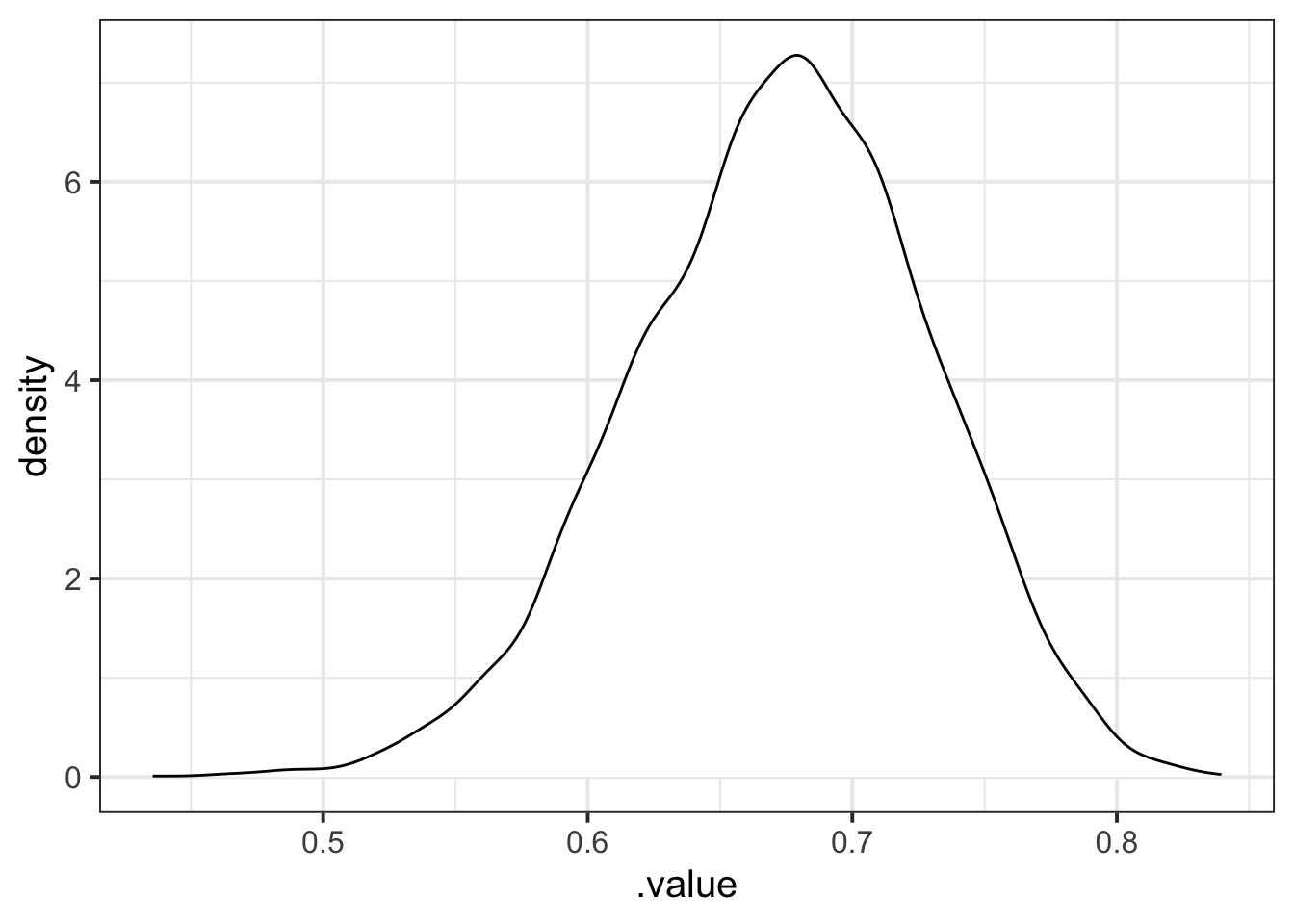
Let’s look at an estimate!

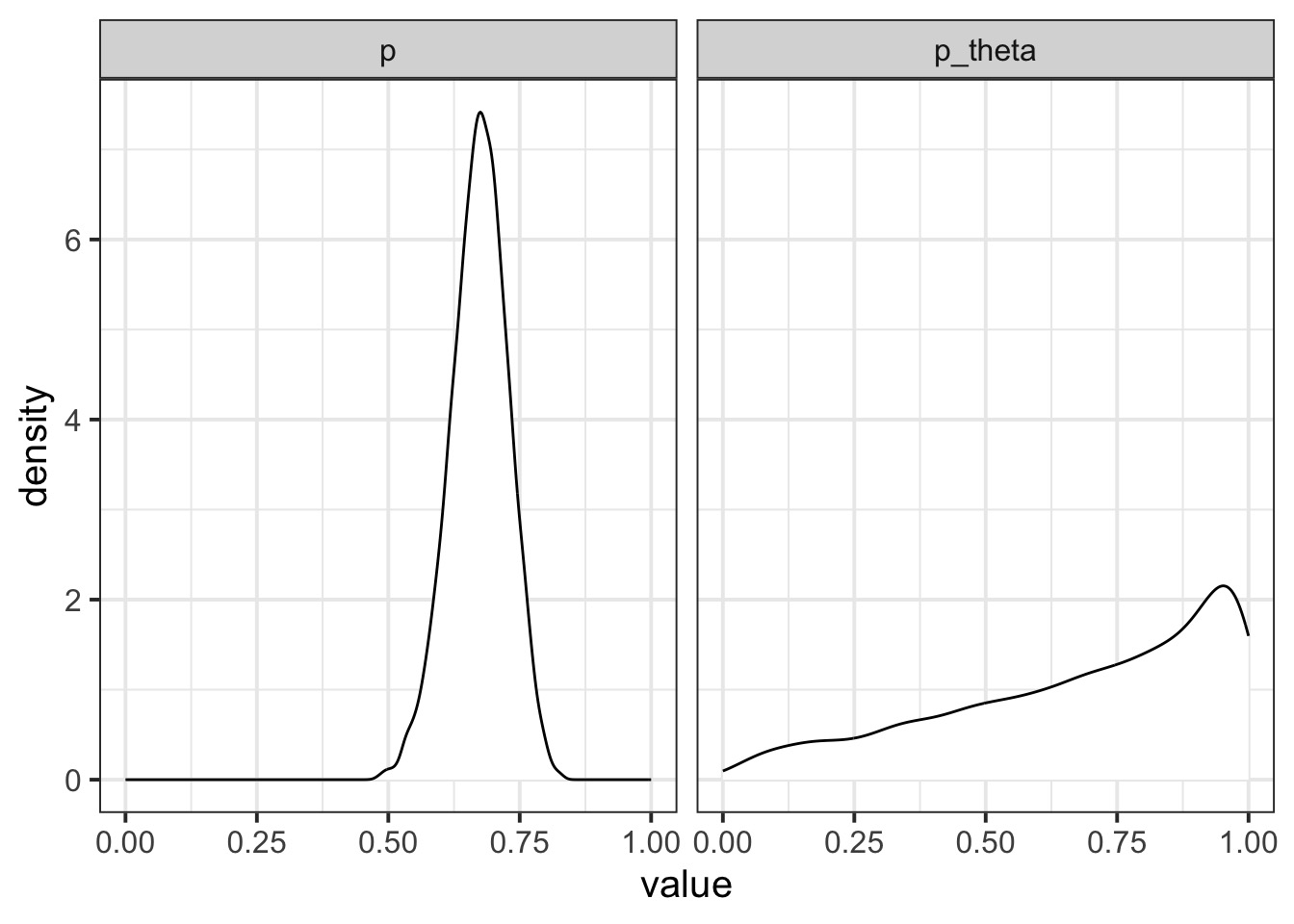
How does Overdispersion Affect this?

Code

d <- 35
d_trans <- (d - mean(reedfrogs$density))/sd(reedfrogs$density)

coef_draws <- tidy_draws(reed_bb_fit) |>
  mutate(p = inv_logit(a + b*d_trans),
         p_theta = rbeta2(n(), p, theta)) |>
  tidyr::pivot_longer(cols = c(p, p_theta))

ggplot(coef_draws,
       aes(x = value)) +
  geom_density(fill = "white") +
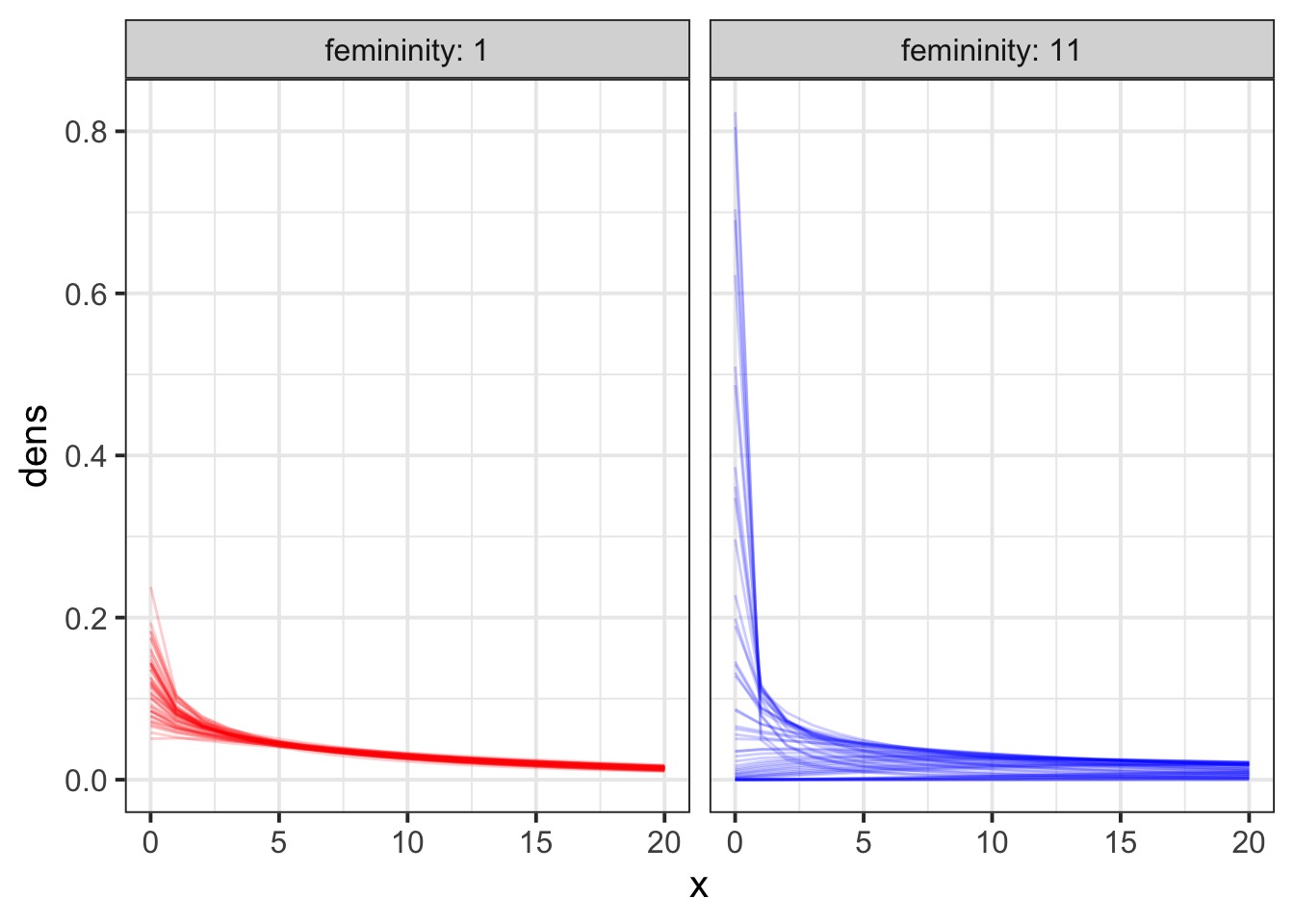
  facet_wrap(vars(name))

Variability in Overdispersion by Draw

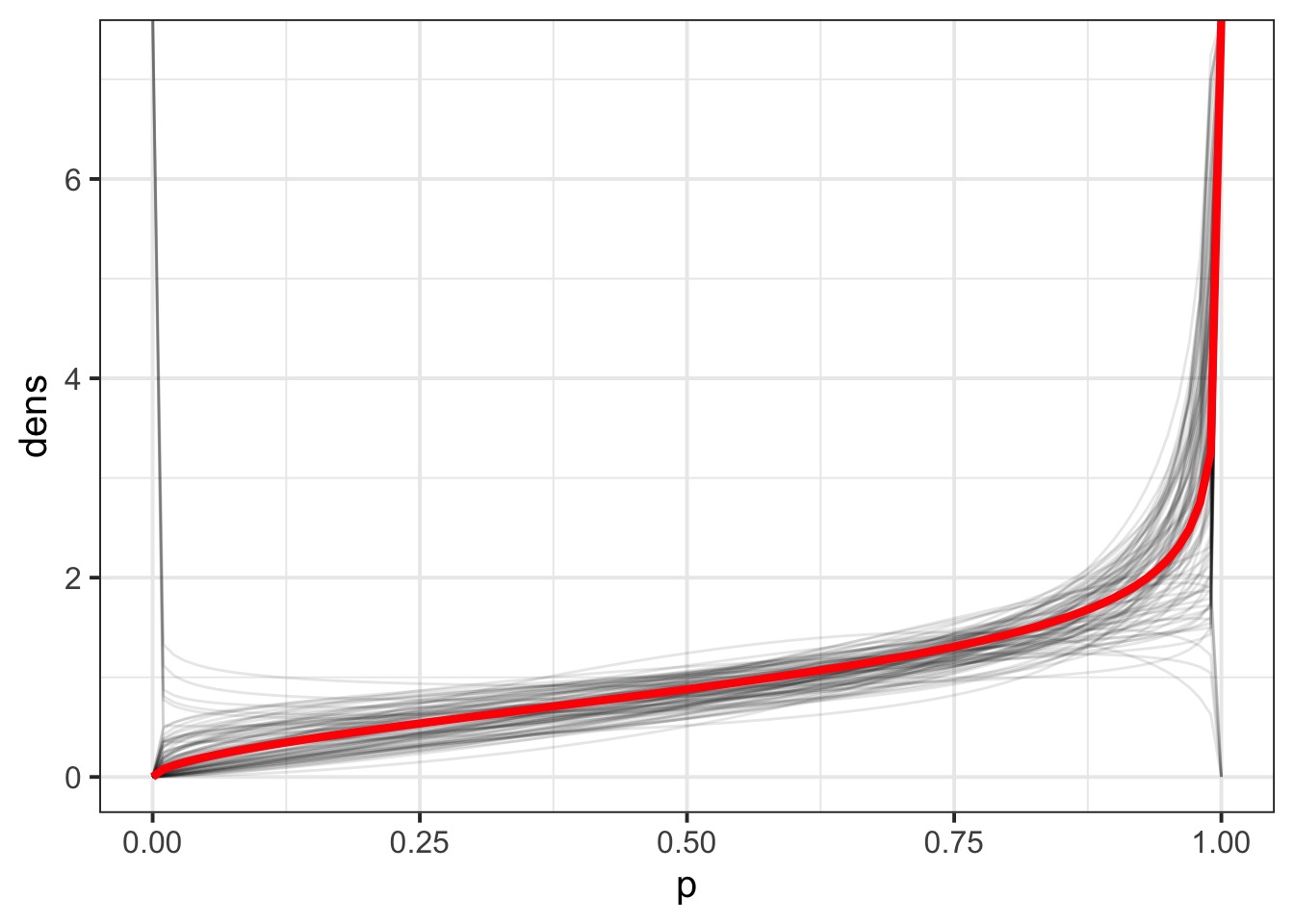
Did this solve our overdispersion problem?

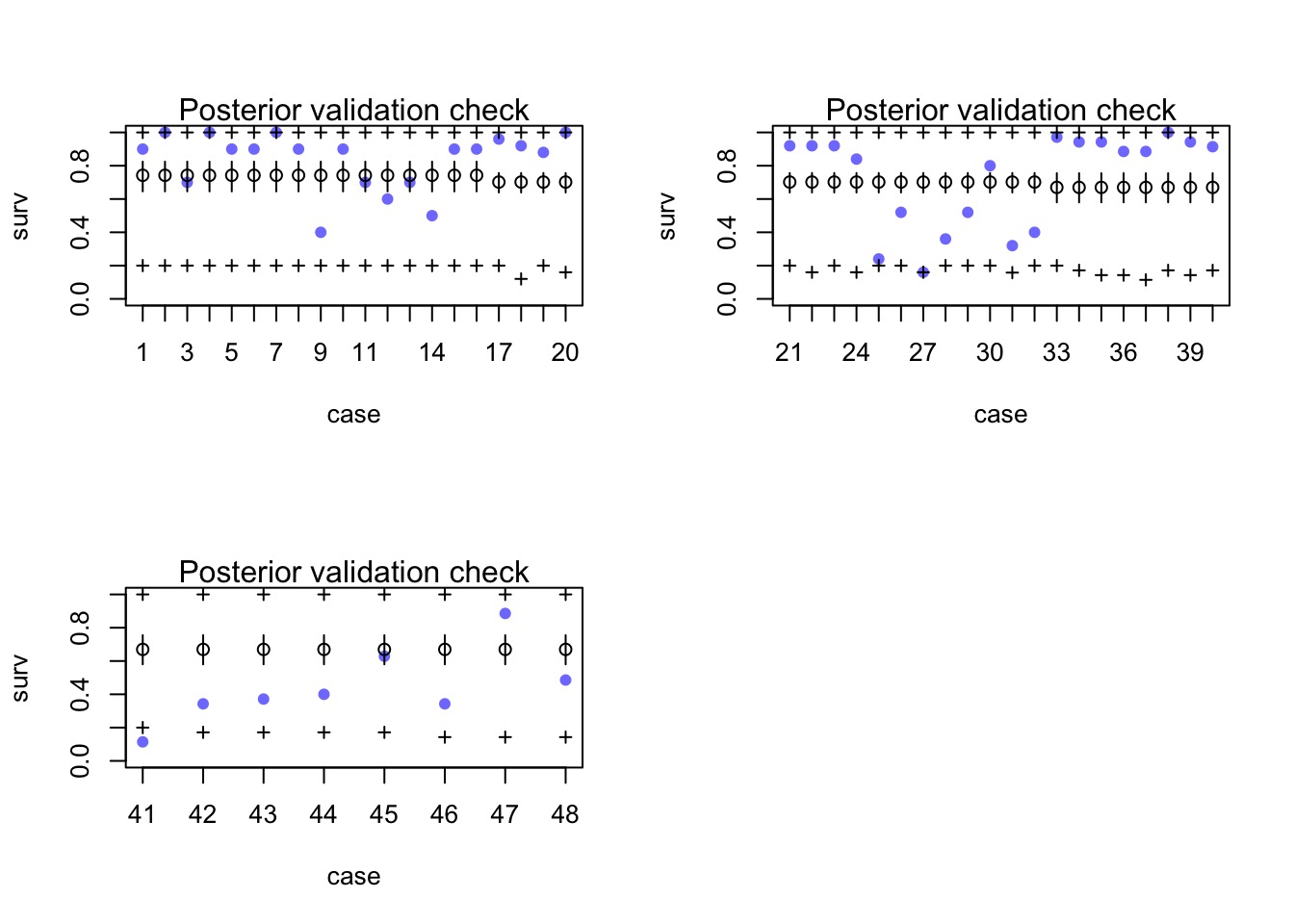
Results

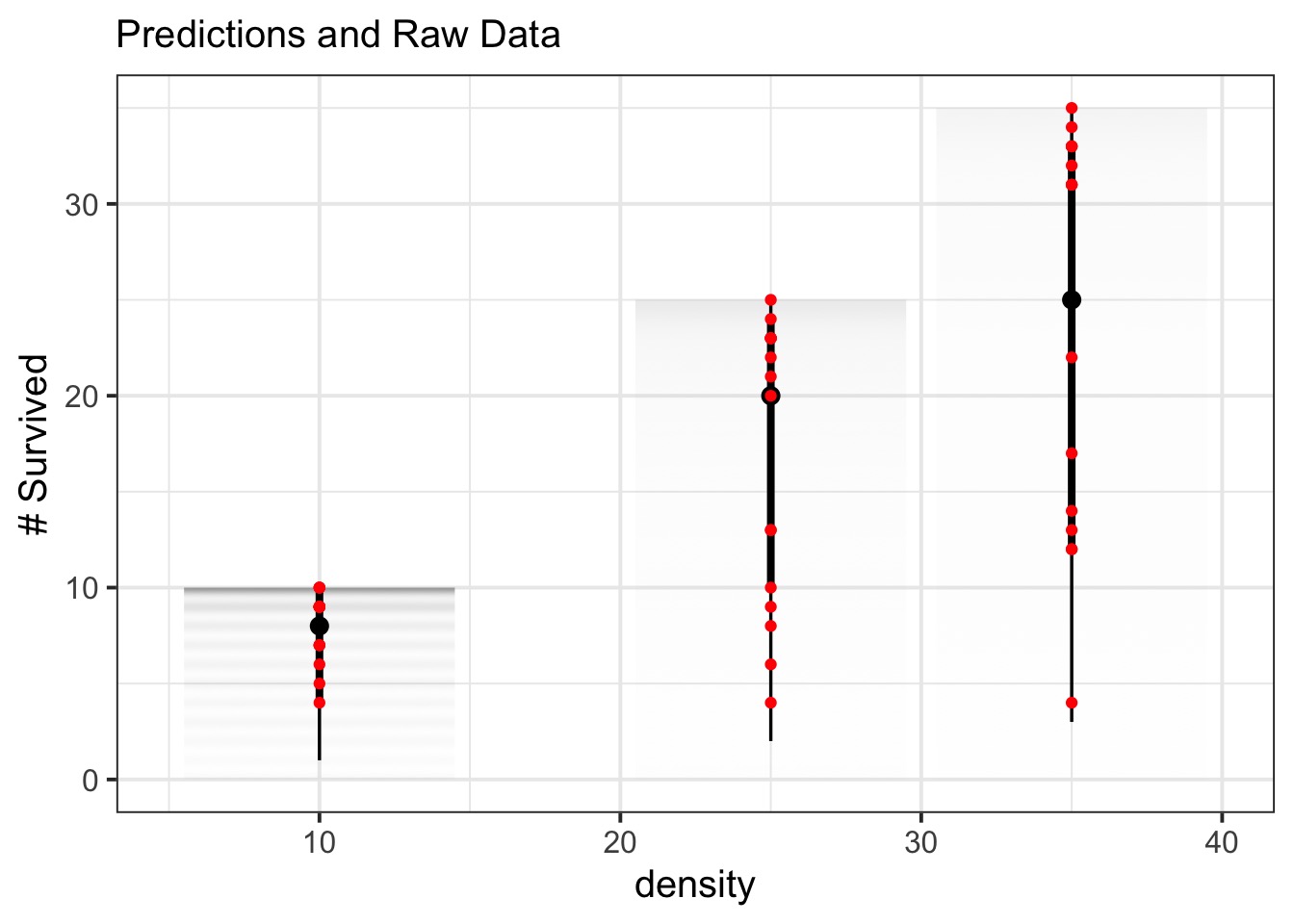
A brief note on IC

• Because of the underlying latent nature of a beta-binomial, use WAIC with care

• DIC and LOO more reliable, but stay tuned.

• But, there are alternate models here with more predictors which might explain away the heterogeneity.

• Also, RE might handle the hetereogeneity, obviating the need for this overdispersion.

Hurricanes and Gamma Poisson

Discover Magazine

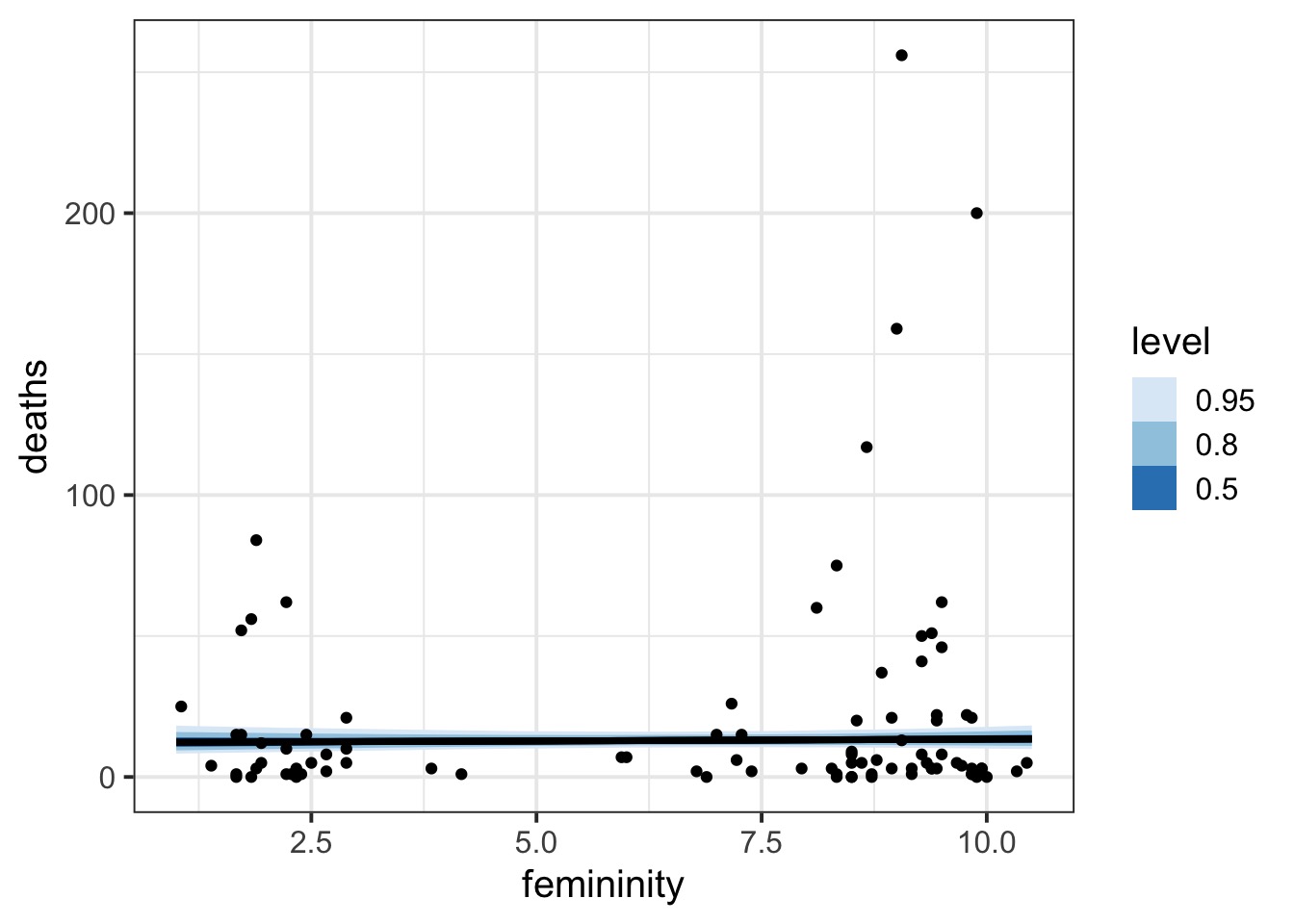
Overdispersed hurricanes

      name year deaths category min_pressure damage_norm female femininity
1     Easy 1950      2        3          960        1590      1    6.77778
2     King 1950      4        3          955        5350      0    1.38889
3     Able 1952      3        1          985         150      0    3.83333
4  Barbara 1953      1        1          987          58      1    9.83333
5 Florence 1953      0        1          985          15      1    8.33333
6    Carol 1954     60        3          960       19321      1    8.11111

Overdispersed hurricanes

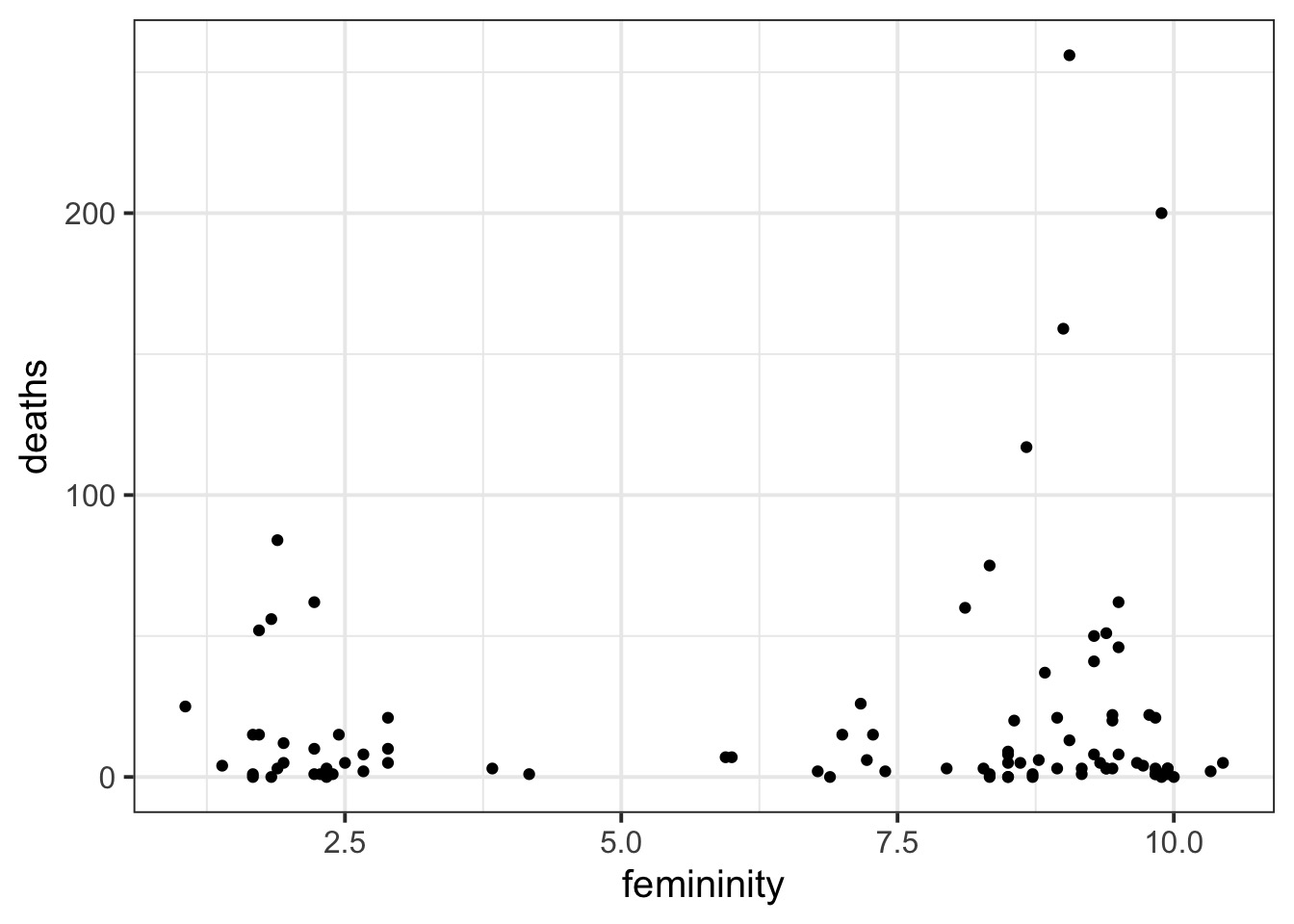
Poisson?

hur_mod <- glm(deaths ~ femininity, family = poisson,
               data = Hurricanes)

plotQQunif(simulateResiduals(hur_mod))

Options for Overdispersed Poisson

• Quasi-poisson
  • \(var(Y) = \theta \mu\)
    
  • Post-hoc fitting of dispersion parameter
• Gamma-poisson mixture
  • \(Y \sim Pois(\lambda)\)
    
  • $Gamma(, )
  • Equivalent to a Negative Binomial
    
  • Variance increases with square of mean

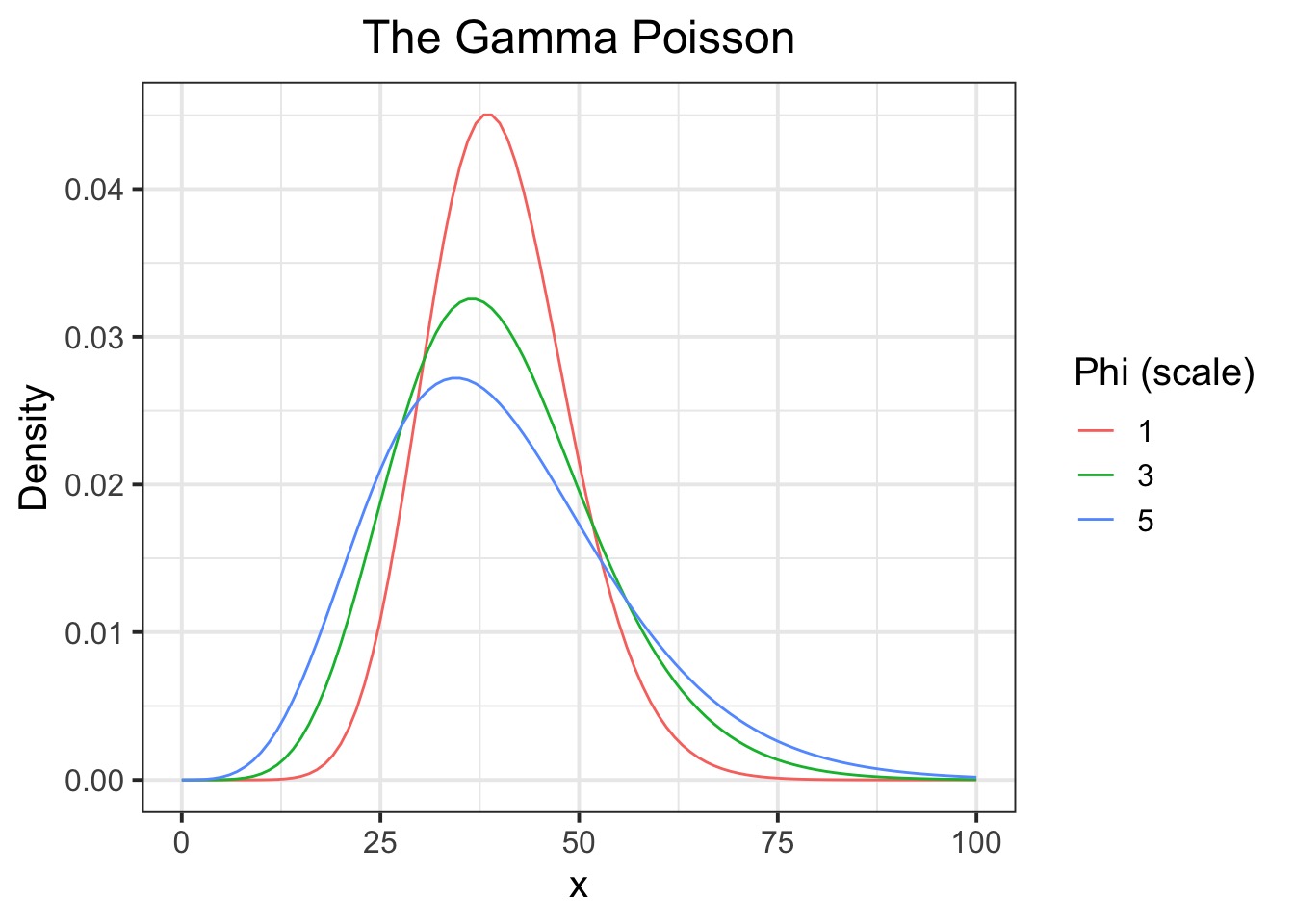
The Gamma Poisson

\[ Y \sim GammaPoisson(\lambda, \phi)\]

• One of the most useful distributions you will run into is the Gamma Poison.

• It’s just another name for the negative binomial.

• Distribution for count data whose variance increases faster than its mean - Variance is \(\lambda + \lambda 2/\phi\)

• The \(\lambda\) parameter of your standard Poisson is Gamma distributed.

The Distribution (mean of 40)

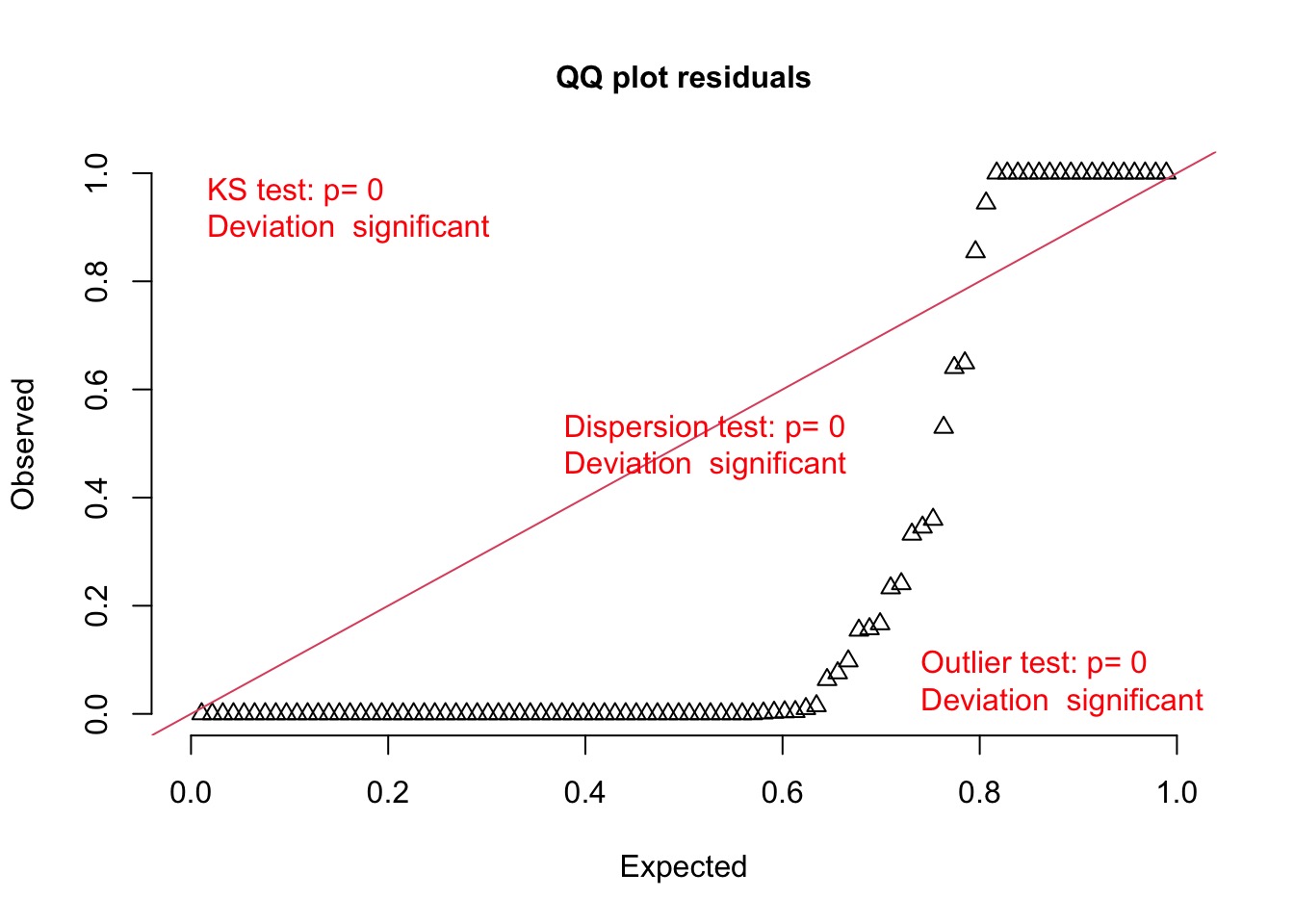
Two approaches to hurricanes with Likelihood

hur_qp<- glm(deaths ~ femininity, 
             family = quasipoisson,
               data = Hurricanes)

library(MASS)
hur_nb <- glm.nb(deaths ~ femininity, 
               data = Hurricanes)

Another look at overdispersion

summary(hur_qp)

Call:
glm(formula = deaths ~ femininity, family = quasipoisson, data = Hurricanes)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.50037    0.54371   4.599 1.38e-05 ***
femininity   0.07387    0.06778   1.090    0.279    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for quasipoisson family taken to be 73.78494)

    Null deviance: 4031.9  on 91  degrees of freedom
Residual deviance: 3937.5  on 90  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 6

How did the Gamma Poisson (NB) Compare?

summary(hur_nb)

Call:
glm.nb(formula = deaths ~ femininity, data = Hurricanes, init.theta = 0.454664691, 
    link = log)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.53050    0.36685   6.898 5.28e-12 ***
femininity   0.06965    0.04882   1.427    0.154    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(0.4547) family taken to be 1)

    Null deviance: 111.15  on 91  degrees of freedom
Residual deviance: 109.10  on 90  degrees of freedom
AIC: 708.63

Number of Fisher Scoring iterations: 1

              Theta:  0.4547 
          Std. Err.:  0.0625 

 2 x log-likelihood:  -702.6260 

Let’s look at the residuals

res_nb <- simulateResiduals(hur_nb)
plotQQunif(res_nb)

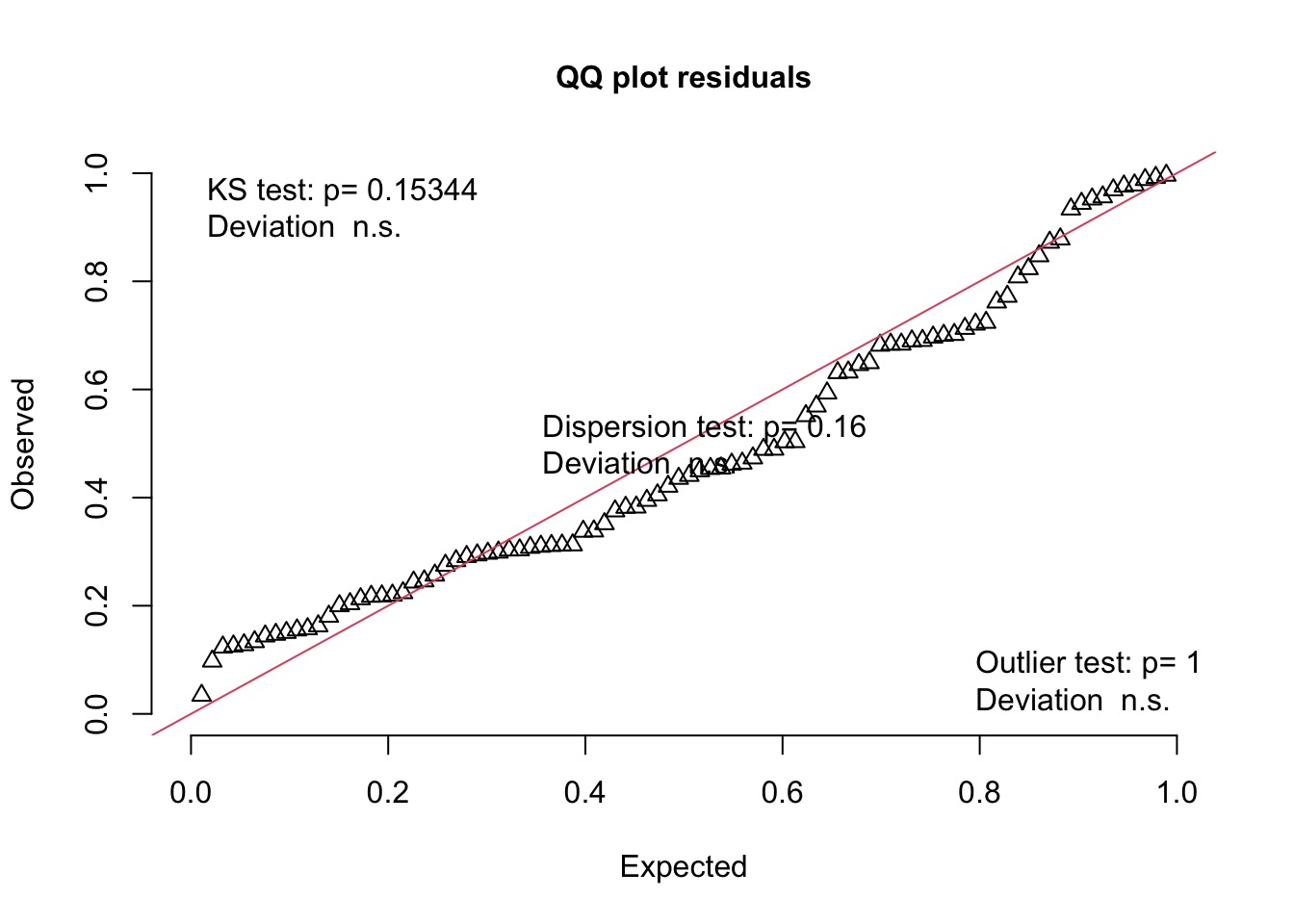
A Fully Bayesian Gamma Poisson

Hurricanes$f <- scale(Hurricanes$femininity)

huric_mod_gp <- alist(
  #likelihood
  deaths ~ dgampois(lambda, scale),
  
  #Data generating process
  log(lambda) <- a + b*f,
  
  #priors
  a ~ dnorm(0,10),
  b ~ dnorm(0,10),
  scale ~ dexp(2)
)

huric_fit_gp <- quap(huric_mod_gp, data=Hurricanes)

Did it Work?

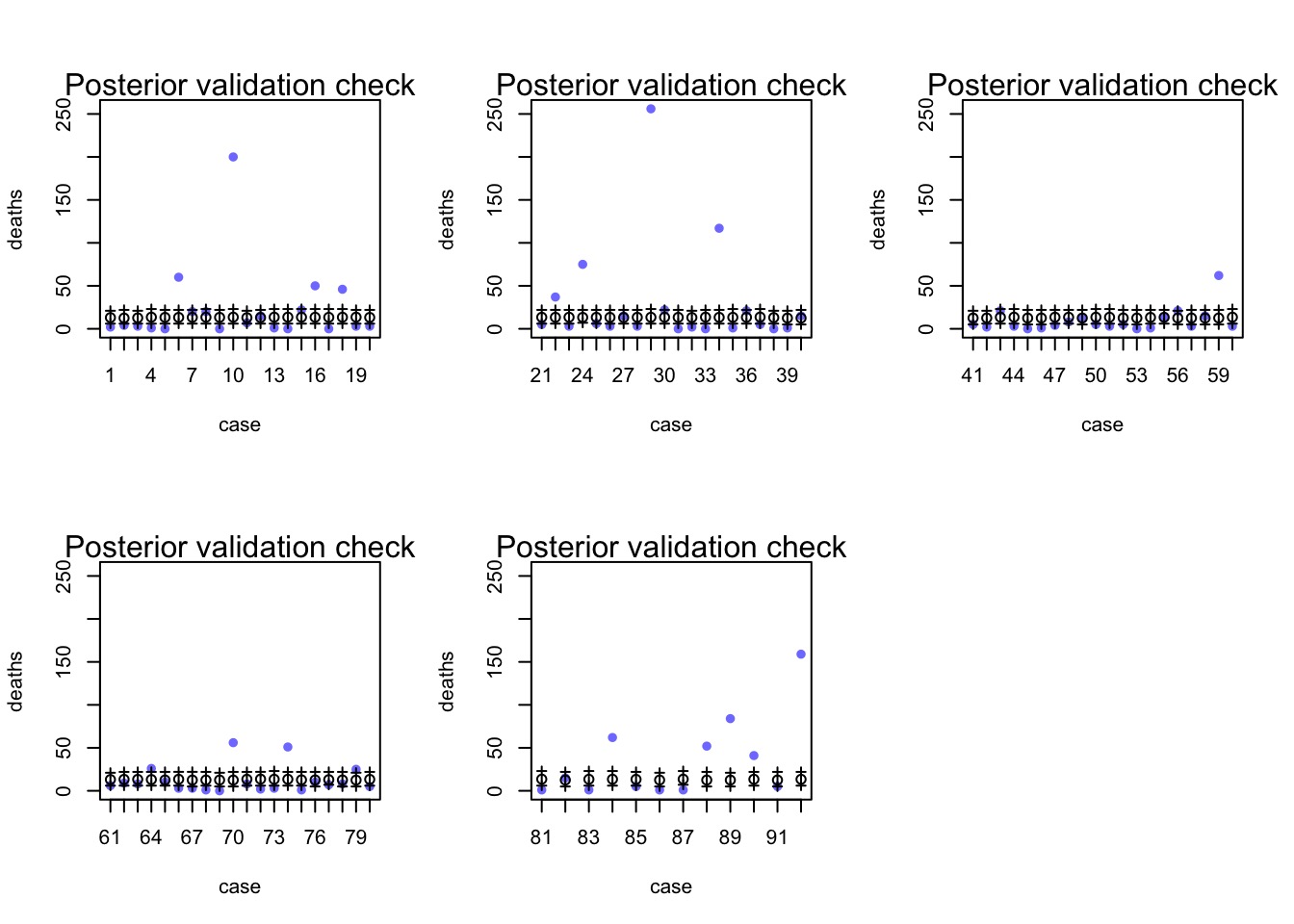
Evaluating Posterior Predictions

Did it Predict Well?

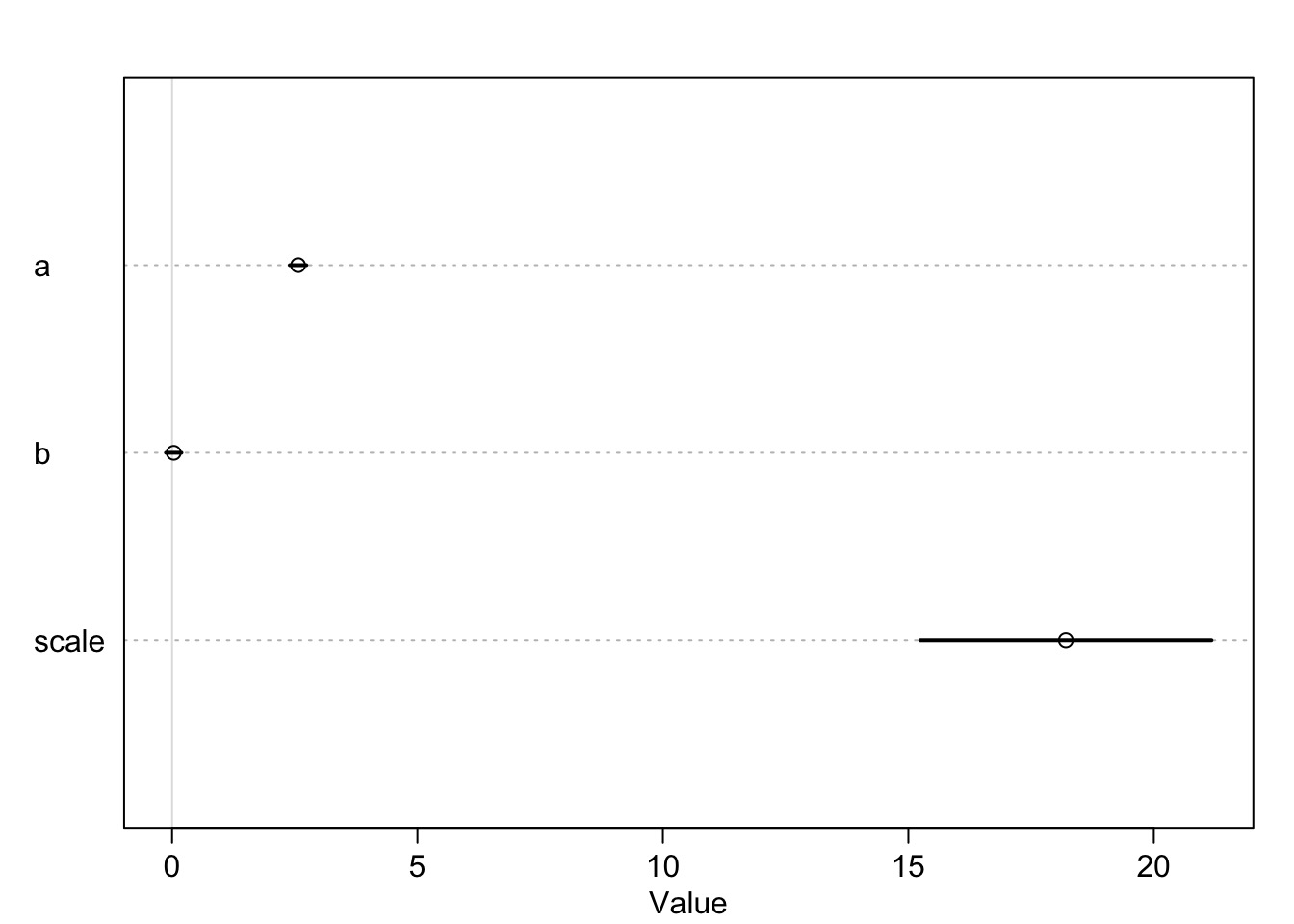
Wait, Those Coefs…

plot(huric_fit_gp)

Well, What did the Predictions Say

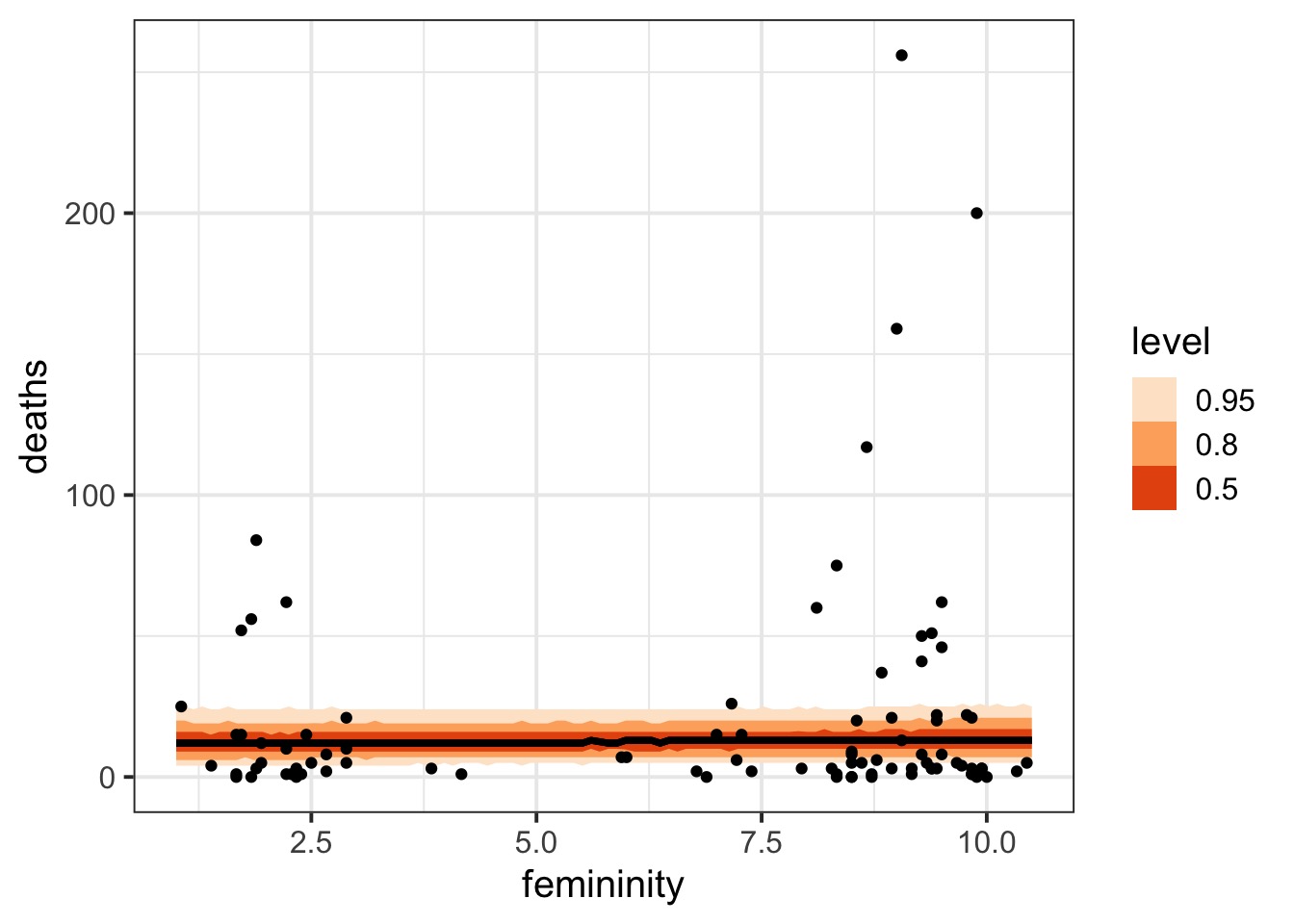
Overdispersion!

• We can use mixtures to model overdispersed data.

• These mixtures then have core parameters of one distribution as part of a second distribution.

• This allows us to flexibly model overdispersion, but, sometimes overdispersion means there are parameters we are not accounting for.

• Think about better models of overdispersion…