Information Theory and a Multimodel World

How complex a model do you need to be useful?

Some models are simple but good enough

More Complex Models are Not Always Better or Right

Our Old Friend \(R^2\), but Bayesian

\[R^2 = \frac{Var_{model}}{Var_{data}}\]

But, with some priors, this can be negative

\[R^2_{bayes} = \frac{Var_{model}}{Var_{model} + Var_{residual}}\]

Is this useful?

A Bayesian R2 Function

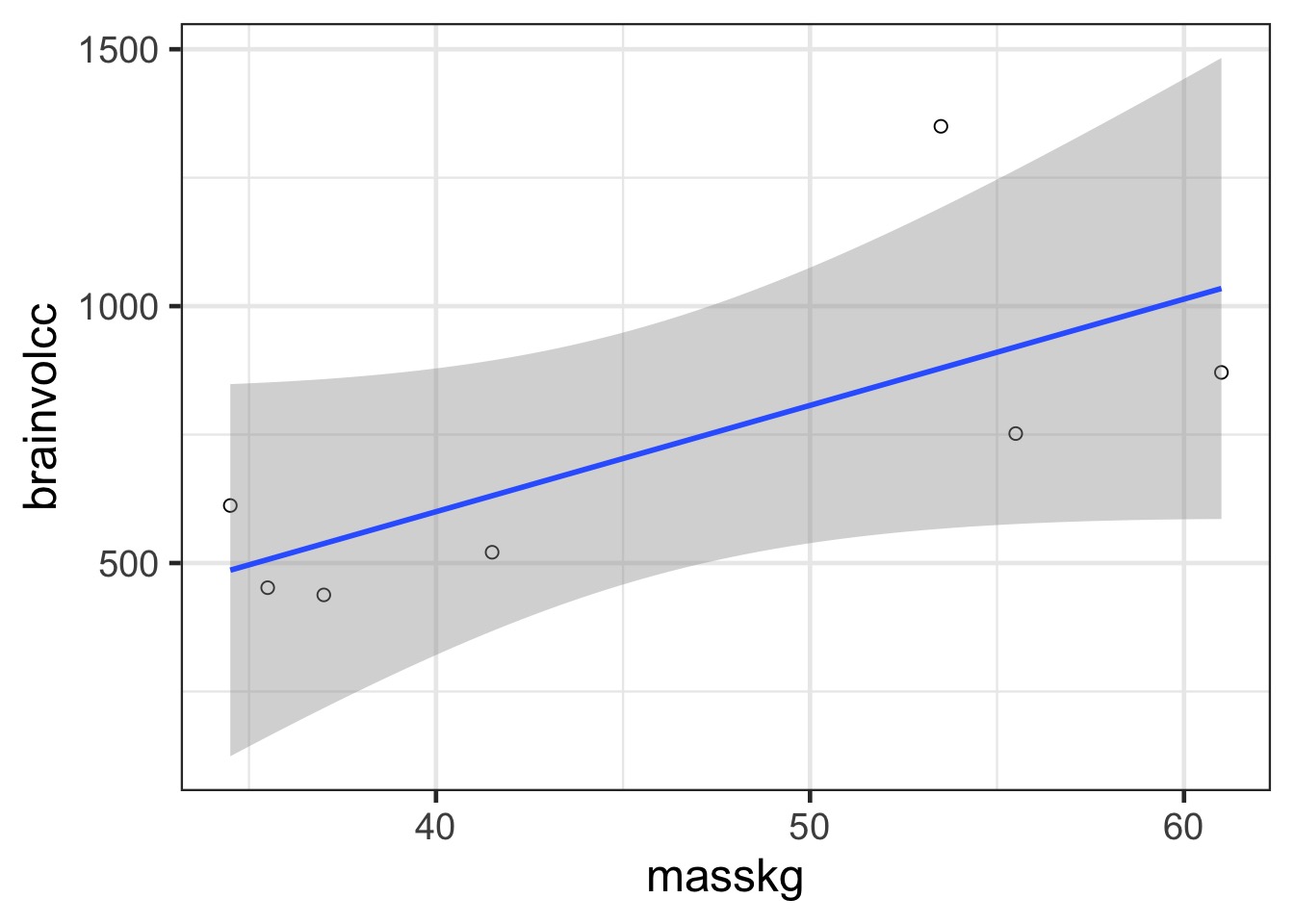
Consider this data…

sppnames <- c( "afarensis","africanus",
               "habilis","boisei",
               "rudolfensis","ergaster","sapiens")

brainvolcc <- c( 438 , 452 , 612, 521, 752, 871, 1350 )
masskg <- c( 37.0 , 35.5 , 34.5 , 41.5 , 55.5 , 61.0 , 53.5 )

d <- data.frame( species=sppnames, 
                 brain=brainvolcc, 
                 mass=masskg )

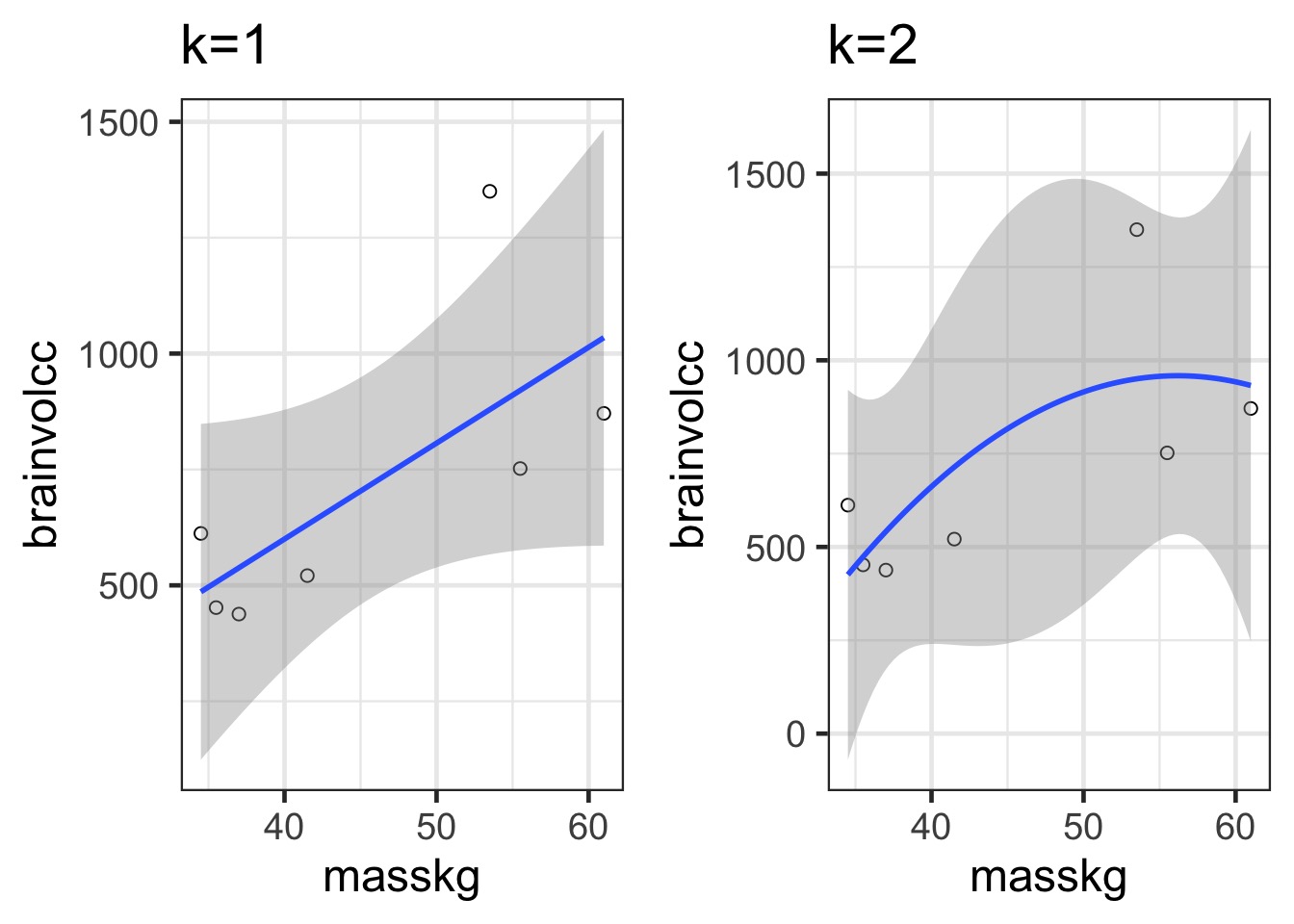
Underfitting

We have explained nothing!

Overfitting

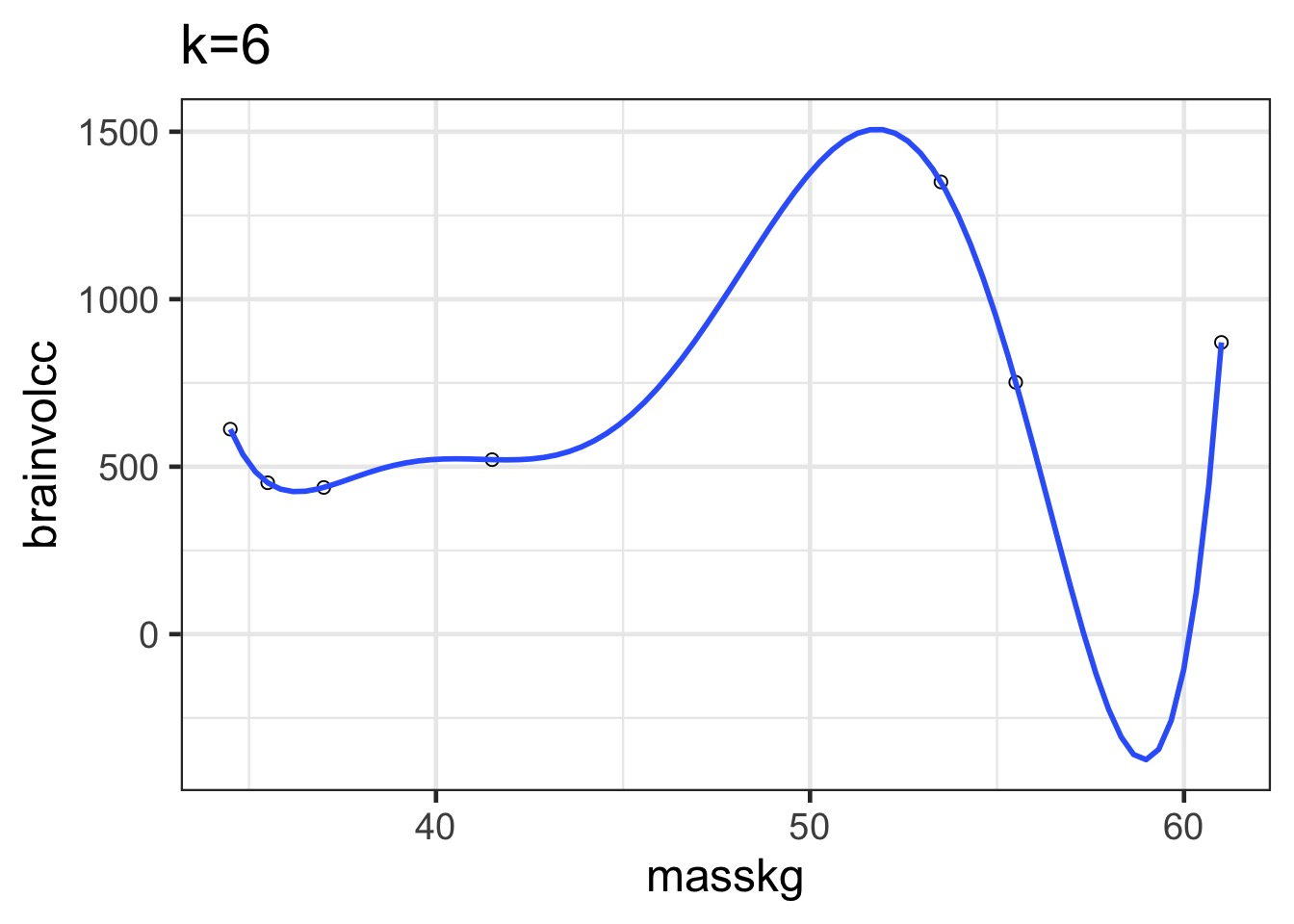
We have perfectly explained this sample

What is the right fit? How do weGet there?

How do we navigate Scylla and Charybdis?

  1. Information theory

  2. Regularization

    • Force parameters to demonstrate they have strong support
    • Penalize parameters with weak support

  3. Optimization for Prediction

    • Cross-Validation
    • Information Theory
    • Drawing from comparison of information loss

Information Theory and Entropy

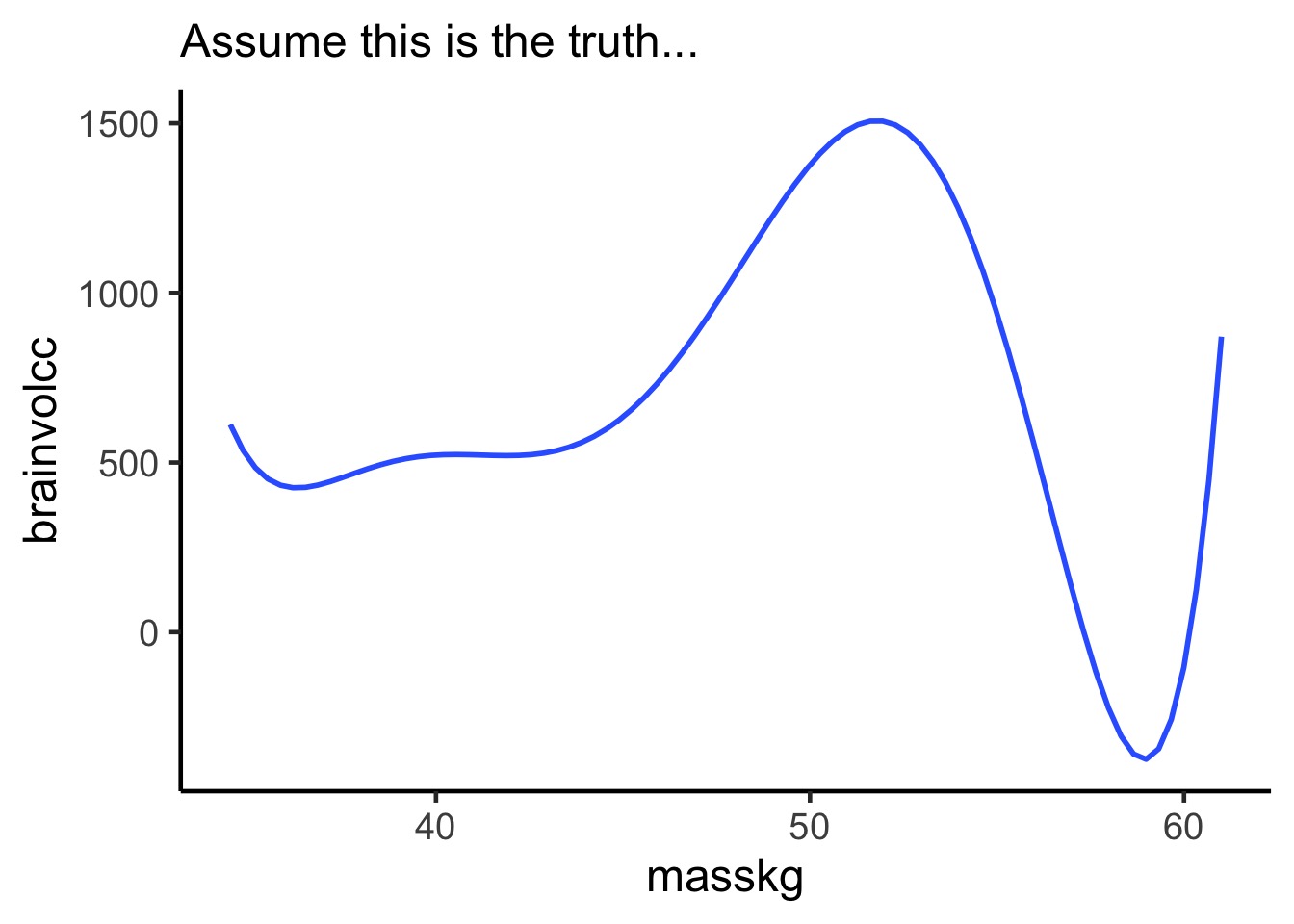
Entropy: Over the distribution of brainvolcc, what is the average log probability of observing values

\[H = - E[log(p_i)] = -\sum p_i log(p_i)\]

  • sum over the curve

  • notice higher entropy the more a wiggly curve as it repeats the same values

  • a straight line will have lower entropy from a uniform distribution

Difference between the truth and a model

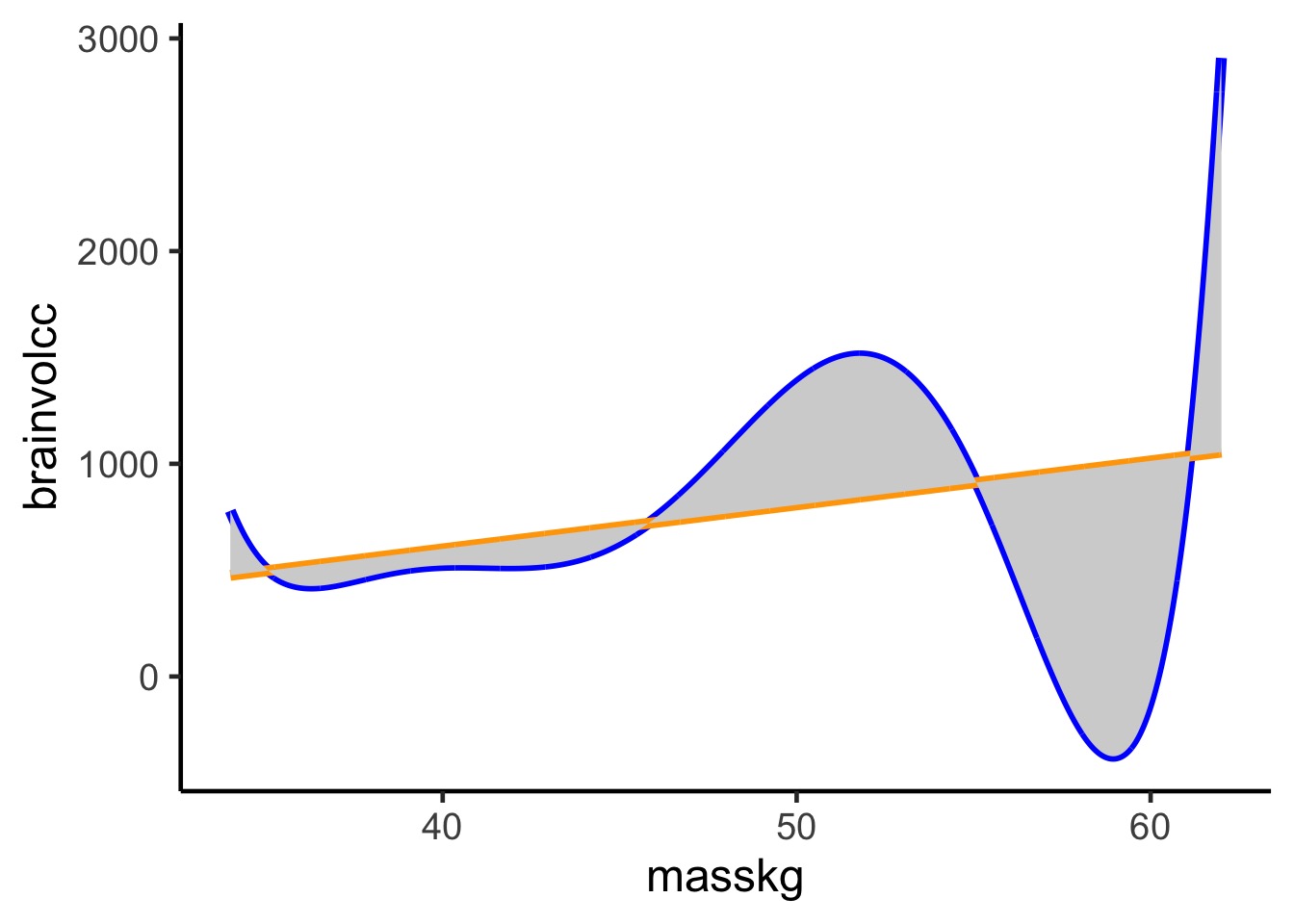
Kullback-Leibler Divergence

Divergence: The additional uncertainty induced by using probabilities from one distribution to describe another distribution.

\[D_{KL} = \sum p_i (log(p_i) − log(q_i)) \\ = \sum p_i log\frac{p_i}{q_i}\] where \(q_i\) is the probability of a value from the model and \(p_i\) from the truth. This is the difference in information caused by using the model to approximate the truth.

But - we want to compare models

Difference in information loss between Model 1 (q) and Model 2 (r)

\[ = \sum p_i (log(p_i) − log(q_i) - \sum p_i (log(p_i) − log(r_i) \\\] \[= \sum p_i log(p_i) − p_i log(p_i) - p_i log(q_i) + p_i log(r_i)\] \[= \sum p_i log(r_i) - p_i log(q_i)\] \[=\sum p_i(log(r_i) - log(q_i))\] \[= E[log (r_i)] - E[log(q_i)]\]

So, What is Our Score of Interest Then?

It’s all about \(E[log(q_i)]\)!

\[S(q) = \sum log(q_i)\]

  • This is the unscaled average of our model score.

  • It is also the log pointwise predictive density.

  • Provides an estimate of how well our model’s predictive accuracy.

  • Pointwise, and uses entire posterior for each observation.

lppd for one point, visually

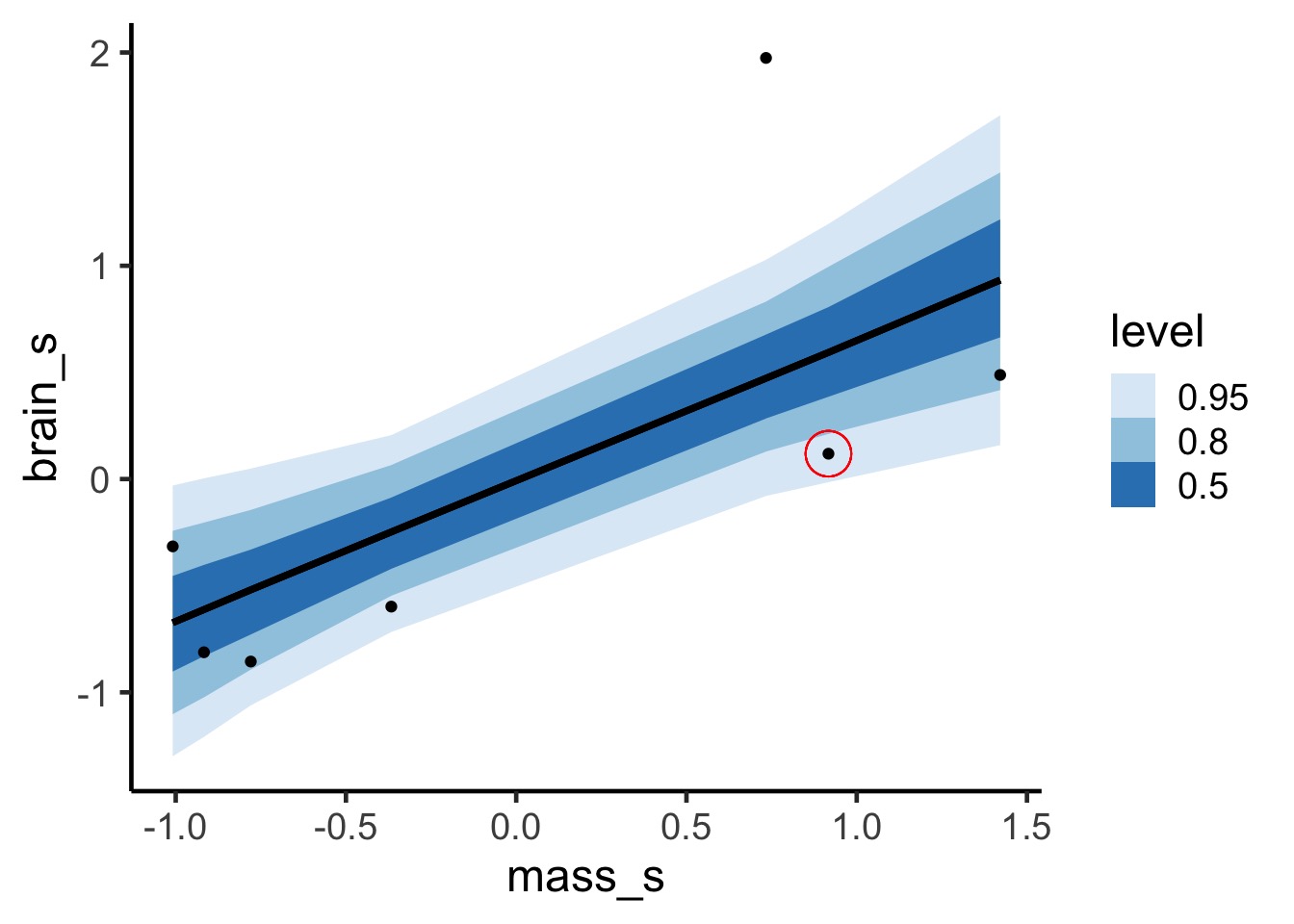
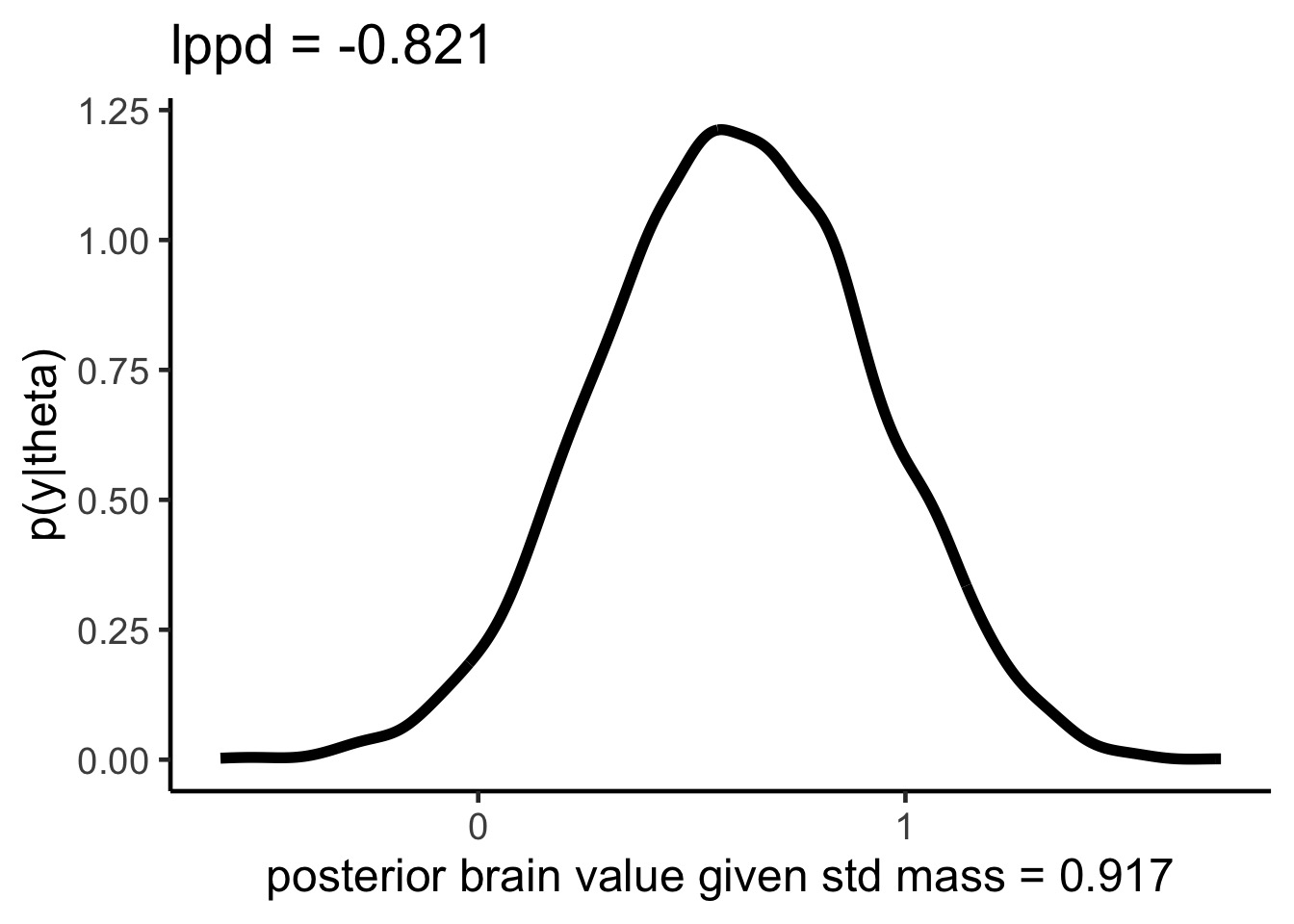
lppd and Deviance

\[ Deviance \approx -2 *lppd\]

  • Hello, old friend.

  • Increasing model complexity will always improve lppd.

  • Out of sample lppd will get worse with model complexity.

In and Out of Sample Deviance

Deviance = -2 * log(dnorm(\(y_i | \mu_i\)))
The deviance of this linear regression is 3.1766285^{5}

In and Out of Sample Deviance

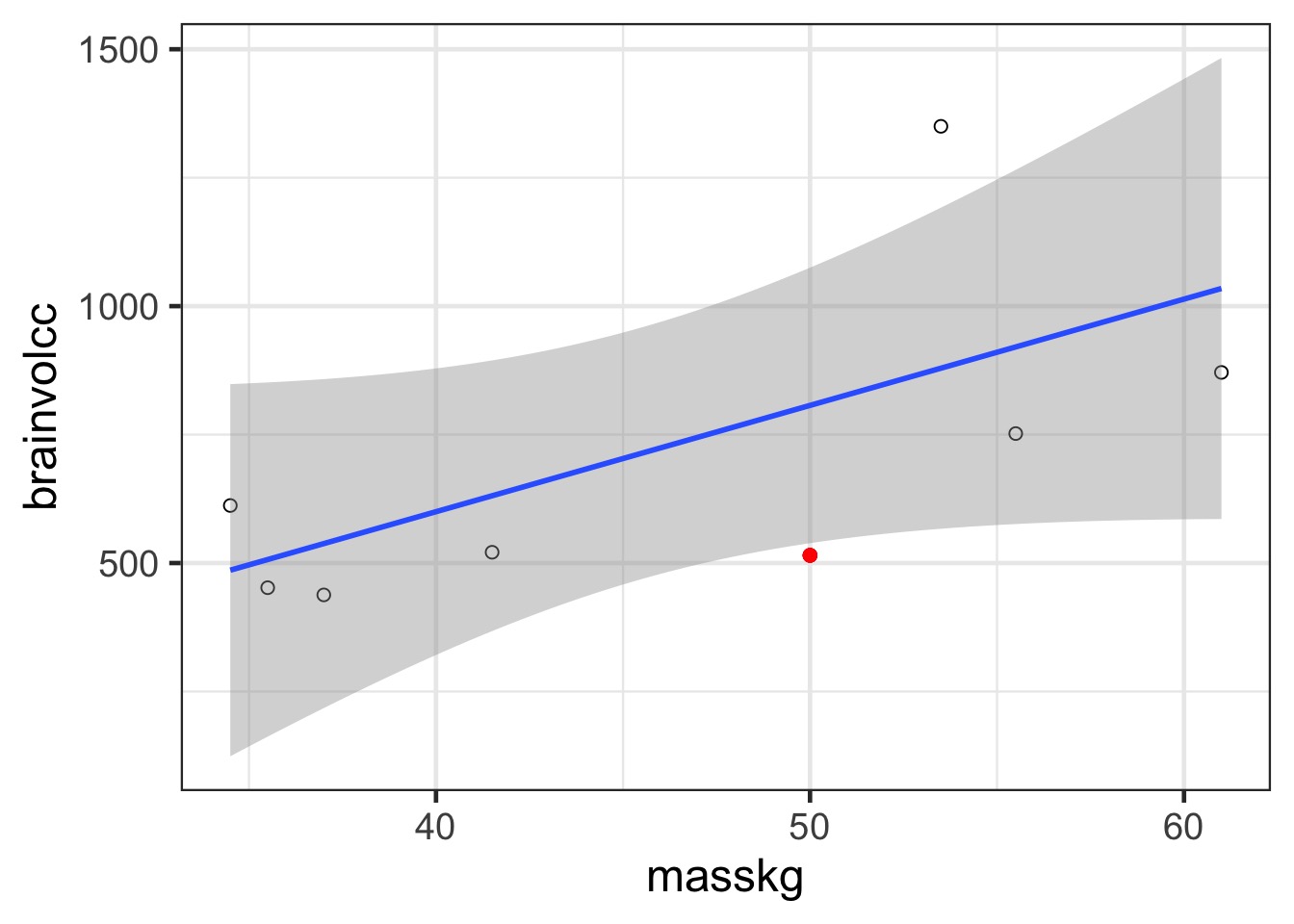
Prediction: 806.8141456, Observe: 515
Deviance: 8.5265838^{4}

In and Out of Sample Deviance

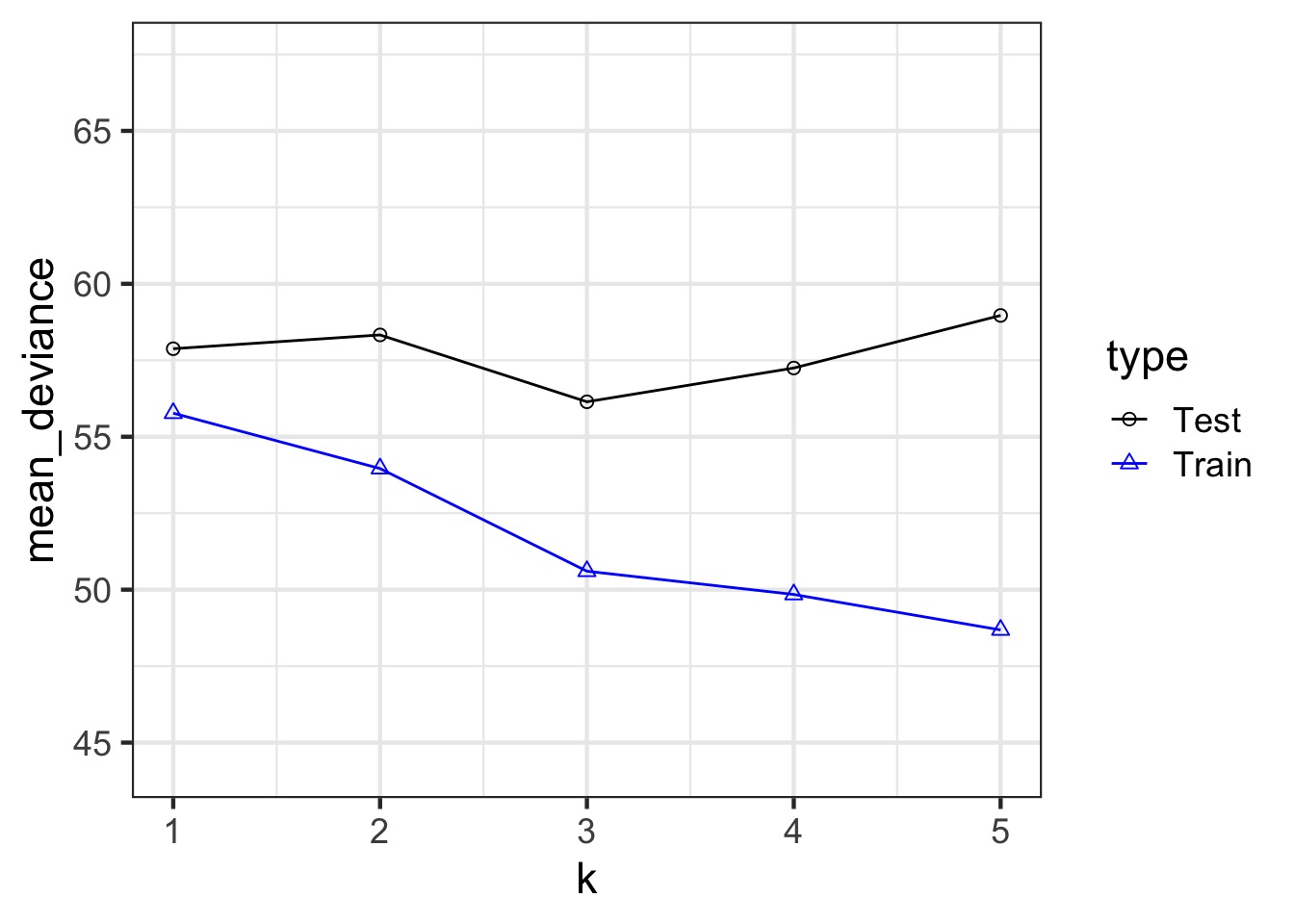
Our Goal for Judging Models

  • Can we minimize the out of sample deviance

  • So, fit a model, and evaluate how different the deviance is for a training versus test data set is

  • What can we use to minimize the difference?

How do we navigate Scylla and Charybdis?

  1. Information theory

  2. Regularization

    • Force parameters to demonstrate they have strong support
    • Penalize parameters with weak support

  3. Optimization for Prediction

    • Cross-Validation
    • Information Theory
    • Drawing from comparison of information loss

Regularlization

List of 97
 $ line                      :List of 6
  ..$ colour       : chr "black"
  ..$ linewidth    : num 0.773
  ..$ linetype     : num 1
  ..$ lineend      : chr "butt"
  ..$ arrow        : logi FALSE
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_line" "element"
 $ rect                      :List of 5
  ..$ fill         : chr "white"
  ..$ colour       : chr "black"
  ..$ linewidth    : num 0.773
  ..$ linetype     : num 1
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ text                      :List of 11
  ..$ family       : chr ""
  ..$ face         : chr "plain"
  ..$ colour       : chr "black"
  ..$ size         : num 17
  ..$ hjust        : num 0.5
  ..$ vjust        : num 0.5
  ..$ angle        : num 0
  ..$ lineheight   : num 0.9
  ..$ margin       : 'margin' num [1:4] 0points 0points 0points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : logi FALSE
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ title                     : NULL
 $ aspect.ratio              : NULL
 $ axis.title                : NULL
 $ axis.title.x              :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : num 1
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 4.25points 0points 0points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.title.x.top          :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : num 0
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 0points 4.25points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.title.x.bottom       : NULL
 $ axis.title.y              :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : num 1
  ..$ angle        : num 90
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 4.25points 0points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.title.y.left         : NULL
 $ axis.title.y.right        :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : num 0
  ..$ angle        : num -90
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 0points 0points 4.25points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.text                 :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : chr "grey30"
  ..$ size         : 'rel' num 0.8
  ..$ hjust        : NULL
  ..$ vjust        : NULL
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : NULL
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.text.x               :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : num 1
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 3.4points 0points 0points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.text.x.top           :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : num 0
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 0points 3.4points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.text.x.bottom        : NULL
 $ axis.text.y               :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : num 1
  ..$ vjust        : NULL
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 3.4points 0points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.text.y.left          : NULL
 $ axis.text.y.right         :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : num 0
  ..$ vjust        : NULL
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 0points 0points 3.4points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ axis.ticks                :List of 6
  ..$ colour       : chr "grey20"
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ lineend      : NULL
  ..$ arrow        : logi FALSE
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_line" "element"
 $ axis.ticks.x              : NULL
 $ axis.ticks.x.top          : NULL
 $ axis.ticks.x.bottom       : NULL
 $ axis.ticks.y              : NULL
 $ axis.ticks.y.left         : NULL
 $ axis.ticks.y.right        : NULL
 $ axis.ticks.length         : 'simpleUnit' num 4.25points
  ..- attr(*, "unit")= int 8
 $ axis.ticks.length.x       : NULL
 $ axis.ticks.length.x.top   : NULL
 $ axis.ticks.length.x.bottom: NULL
 $ axis.ticks.length.y       : NULL
 $ axis.ticks.length.y.left  : NULL
 $ axis.ticks.length.y.right : NULL
 $ axis.line                 : list()
  ..- attr(*, "class")= chr [1:2] "element_blank" "element"
 $ axis.line.x               : NULL
 $ axis.line.x.top           : NULL
 $ axis.line.x.bottom        : NULL
 $ axis.line.y               : NULL
 $ axis.line.y.left          : NULL
 $ axis.line.y.right         : NULL
 $ legend.background         :List of 5
  ..$ fill         : NULL
  ..$ colour       : logi NA
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ legend.margin             : 'margin' num [1:4] 8.5points 8.5points 8.5points 8.5points
  ..- attr(*, "unit")= int 8
 $ legend.spacing            : 'simpleUnit' num 17points
  ..- attr(*, "unit")= int 8
 $ legend.spacing.x          : NULL
 $ legend.spacing.y          : NULL
 $ legend.key                :List of 5
  ..$ fill         : chr "white"
  ..$ colour       : logi NA
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ legend.key.size           : 'simpleUnit' num 1.2lines
  ..- attr(*, "unit")= int 3
 $ legend.key.height         : NULL
 $ legend.key.width          : NULL
 $ legend.text               :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : 'rel' num 0.8
  ..$ hjust        : NULL
  ..$ vjust        : NULL
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : NULL
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ legend.text.align         : NULL
 $ legend.title              :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : num 0
  ..$ vjust        : NULL
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : NULL
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ legend.title.align        : NULL
 $ legend.position           : chr "right"
 $ legend.direction          : NULL
 $ legend.justification      : chr "center"
 $ legend.box                : NULL
 $ legend.box.just           : NULL
 $ legend.box.margin         : 'margin' num [1:4] 0cm 0cm 0cm 0cm
  ..- attr(*, "unit")= int 1
 $ legend.box.background     : list()
  ..- attr(*, "class")= chr [1:2] "element_blank" "element"
 $ legend.box.spacing        : 'simpleUnit' num 17points
  ..- attr(*, "unit")= int 8
 $ panel.background          :List of 5
  ..$ fill         : chr "white"
  ..$ colour       : logi NA
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ panel.border              :List of 5
  ..$ fill         : logi NA
  ..$ colour       : chr "grey20"
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ panel.spacing             : 'simpleUnit' num 8.5points
  ..- attr(*, "unit")= int 8
 $ panel.spacing.x           : NULL
 $ panel.spacing.y           : NULL
 $ panel.grid                :List of 6
  ..$ colour       : chr "grey92"
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ lineend      : NULL
  ..$ arrow        : logi FALSE
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_line" "element"
 $ panel.grid.major          : NULL
 $ panel.grid.minor          :List of 6
  ..$ colour       : NULL
  ..$ linewidth    : 'rel' num 0.5
  ..$ linetype     : NULL
  ..$ lineend      : NULL
  ..$ arrow        : logi FALSE
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_line" "element"
 $ panel.grid.major.x        : NULL
 $ panel.grid.major.y        : NULL
 $ panel.grid.minor.x        : NULL
 $ panel.grid.minor.y        : NULL
 $ panel.ontop               : logi FALSE
 $ plot.background           :List of 5
  ..$ fill         : NULL
  ..$ colour       : chr "white"
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ plot.title                :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : 'rel' num 1.2
  ..$ hjust        : num 0
  ..$ vjust        : num 1
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 0points 8.5points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ plot.title.position       : chr "panel"
 $ plot.subtitle             :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : num 0
  ..$ vjust        : num 1
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 0points 0points 8.5points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ plot.caption              :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : 'rel' num 0.8
  ..$ hjust        : num 1
  ..$ vjust        : num 1
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 8.5points 0points 0points 0points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ plot.caption.position     : chr "panel"
 $ plot.tag                  :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : 'rel' num 1.2
  ..$ hjust        : num 0.5
  ..$ vjust        : num 0.5
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : NULL
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ plot.tag.position         : chr "topleft"
 $ plot.margin               : 'margin' num [1:4] 8.5points 8.5points 8.5points 8.5points
  ..- attr(*, "unit")= int 8
 $ strip.background          :List of 5
  ..$ fill         : chr "grey85"
  ..$ colour       : chr "grey20"
  ..$ linewidth    : NULL
  ..$ linetype     : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_rect" "element"
 $ strip.background.x        : NULL
 $ strip.background.y        : NULL
 $ strip.clip                : chr "inherit"
 $ strip.placement           : chr "inside"
 $ strip.text                :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : chr "grey10"
  ..$ size         : 'rel' num 0.8
  ..$ hjust        : NULL
  ..$ vjust        : NULL
  ..$ angle        : NULL
  ..$ lineheight   : NULL
  ..$ margin       : 'margin' num [1:4] 6.8points 6.8points 6.8points 6.8points
  .. ..- attr(*, "unit")= int 8
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ strip.text.x              : NULL
 $ strip.text.x.bottom       : NULL
 $ strip.text.x.top          : NULL
 $ strip.text.y              :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : NULL
  ..$ angle        : num -90
  ..$ lineheight   : NULL
  ..$ margin       : NULL
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ strip.text.y.left         :List of 11
  ..$ family       : NULL
  ..$ face         : NULL
  ..$ colour       : NULL
  ..$ size         : NULL
  ..$ hjust        : NULL
  ..$ vjust        : NULL
  ..$ angle        : num 90
  ..$ lineheight   : NULL
  ..$ margin       : NULL
  ..$ debug        : NULL
  ..$ inherit.blank: logi TRUE
  ..- attr(*, "class")= chr [1:2] "element_text" "element"
 $ strip.text.y.right        : NULL
 $ strip.switch.pad.grid     : 'simpleUnit' num 4.25points
  ..- attr(*, "unit")= int 8
 $ strip.switch.pad.wrap     : 'simpleUnit' num 4.25points
  ..- attr(*, "unit")= int 8
 - attr(*, "class")= chr [1:2] "theme" "gg"
 - attr(*, "complete")= logi TRUE
 - attr(*, "validate")= logi TRUE

Regularization and Train-Test Deviance

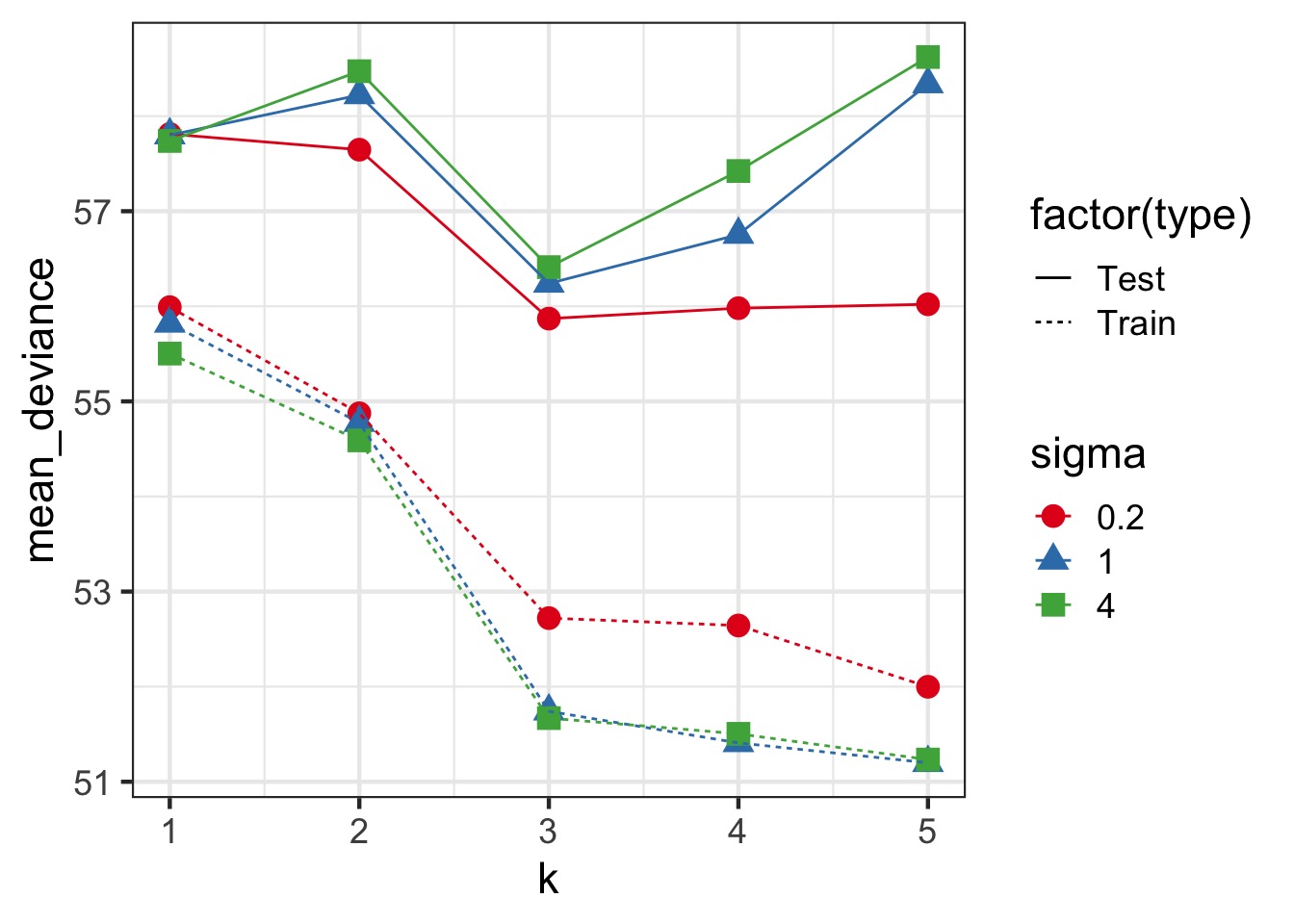
How do we navigate Scylla and Charybdis?

  1. Information theory

  2. Regularization

    • Force parameters to demonstrate they have strong support
    • Penalize parameters with weak support

  3. Optimization for Prediction

    • Cross-Validation
    • Information Theory
    • Drawing from comparison of information loss

A Criteria Estimating Test Sample Deviance

  • What if we could estimate out of sample deviance?

  • The difference between training and testing deviance shows overfitting

A Criteria Estimating Test Sample Deviance

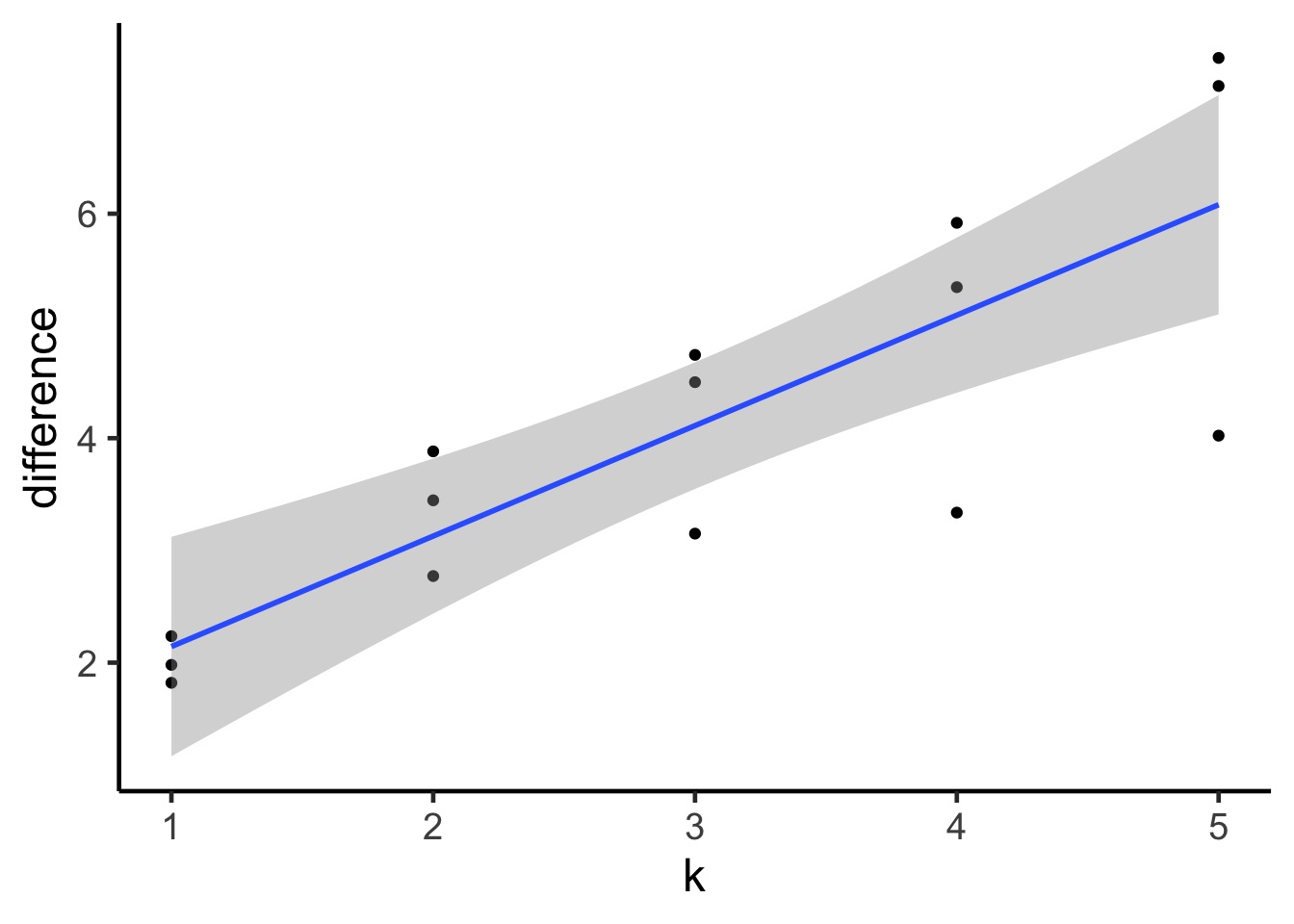
Slope here of 0.98

AIC

  • So, \(E[D_{test}] = D_{train} + 2K\)

  • This is Akaike’s Information Criteria (AIC)

\[AIC = Deviance + 2K\]

AIC

  • Estimate of Leave One Out Cross-Validation

  • AIC optimized for forecasting (out of sample deviance)

  • Requires flat priors

  • Assumes large N relative to K

    • AICc for a correction

  • Difficult to define in a mixed model context

What about IC in Bayes?

  • We do estimate the posterior distribution of the deviance

  • Average of the posterior, \(\bar{D}\) is our \(D_{train}\)

  • But what about # of parameters?

    • For a non-mixed model, this is not a concern - just the AIC
    • For a mixed model…trickier

Effective number of Parameters

  • In addition to \(\bar{D}\), there is also \(\hat{D}\)
    • The value of the posterior at the posterior mean
  • Given Bayesian logic:
    • \(\bar{D}\) is our estimate of the out of sample deviance
    • \(\hat{D}\) is our \(D_{train}\)
    • So, \(\bar{D} - \hat{D}\) = number of parameters
  • We term this \(p_D\) for effective number of parameters

DIC

\[DIC = 2 \bar{D} - 2 p_D\]

DIC

\[DIC = 2 \bar{D} - 2 p_D\]

  • Works well for multivariate normal posteriors
  • Handles mixed models
  • Reduces to AIC with flat priors
  • But does not require flat priors - which does interesting things to \(p_D\)!
  • But… fails with anything non-normal, and hot debate on even mixed effects

And so we pause…

  • Our goal is to maximize prediction

  • Why not look at the pieces that make up the deviance

    • The pointwise predictive power of the posterior

  • We can define the Pr(yi | posterior simulations)

    • This tells us the distribution of the predictive power of our posterior for each point
    • \(lppd = \sum log Pr(y_i | \theta)\)

But what about Parameters?

  • We know that as k increases, our uncertainty in coefficients increases

  • As uncertainty increases, Pr(yi | simulations) widens

  • Thus, this variance gives us an effective penalty term

  • \(p_{waic} = \sum Var(log Pr(y_i | \theta))\)

Widely Applicable IC

\[WAIC = -2 \sum log Pr(y_i | \theta) + 2 \sum Var(log Pr(y_i | \theta))\]

\[= -2 lppd + 2 p_{waic}\]

  • Widely Applicable/Wantanabe-Akaike Information Criteria

  • Advantage in being pointwise is that we also get an estimate of uncertainty

  • Disadvantage that inappropriate to use with lagged (spatial or temporal) predictors

But What about Leave One Out?

The problem

\[LOOCV_{Bayes} = \\lppd_{cv} = \\ \sum_{i=1}^N \frac{1}{S} \sum_{s=1}^S log(y_i | \theta_{s, -i})\] Here, i is observation, 1….N and s is draw from our posterior 1….S.

In essence, for each data point:

  • Remove it & refit the model.
  • Calculate the lppd for that refit.
  • Sum it over each refit.
  • Let your computer warm your house.

Don’t wait to weight!

  • We can do the same if we weighted the lppd of each point by it’s importance.

  • Importance can be defined as \(\frac{p(y_i | \theta_{s, -i})}{p(y_i | \theta_{s})}\)

  • Proportional to just \(\frac{1}{p(y_i | \theta_{s})} = r_s\)

  • Can weight each element of lppd and then standardize by sum of weights.

  • BUT - if we get weird weights, this can cause huge problems

Introducing, the Pareto Distribution

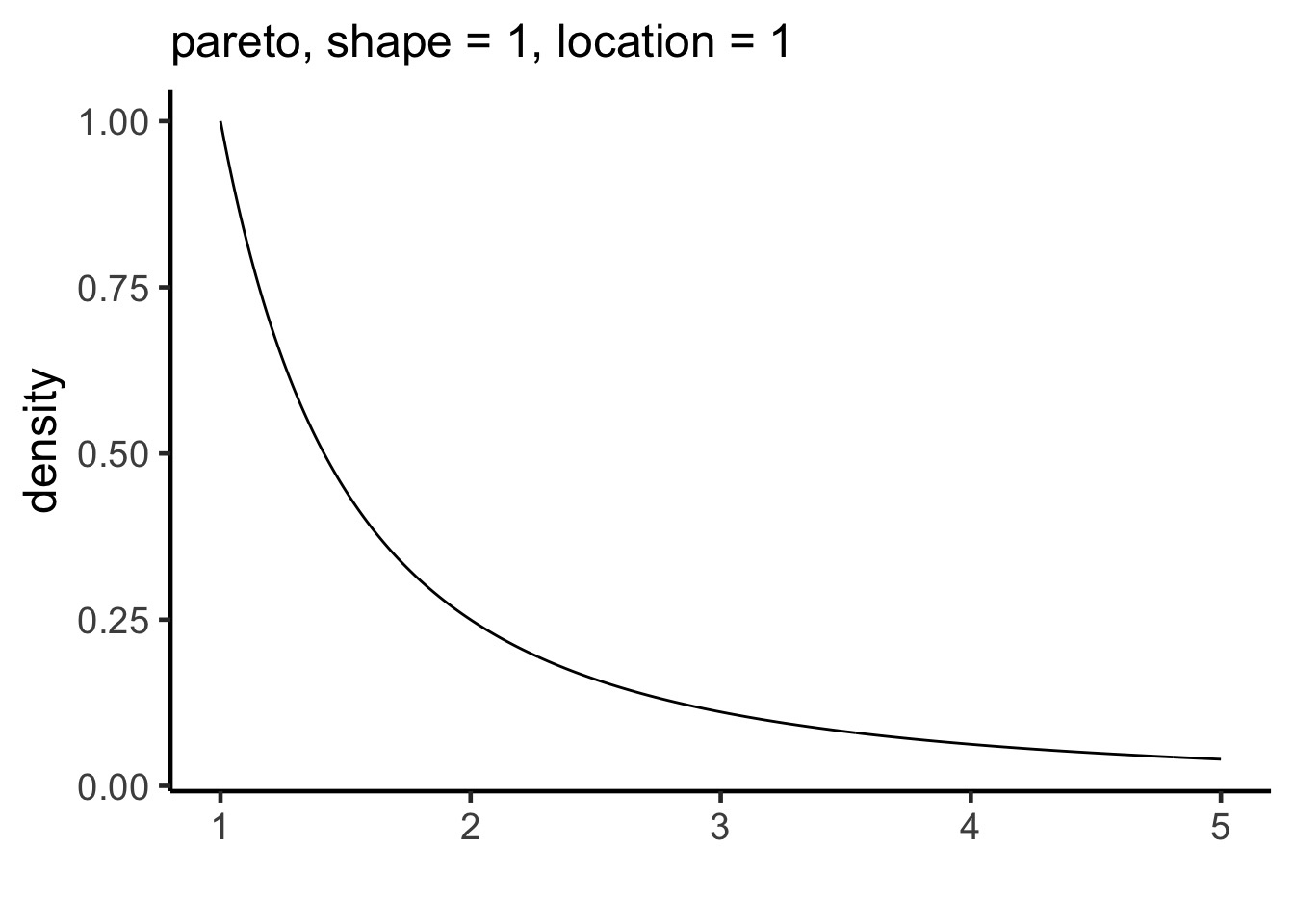
  • Distribution of importances - 80:20 rule

  • For each observation, we can use the largest importance value, and calculate a smoothed Pareto curve of weights

  • PSIS: Pareto Smoothed Importance Sampling

Which should I use?

  • They are all pretty darned similar!

  • WAIC performs better at lower sample sizes.

  • WAIC also can perform better in some nonlinear cases.

  • But, PSIS will also give you information about points driving performance and problems.

How do I use my IC?

We can use difference between fits or calculate:

\[w_{i} = \frac{e^{\Delta_{i}/2 }}{\displaystyle \sum^R_{r=1} e^{\Delta_{i}/2 }}\]
Where \(w_{i}\) is the relative support for model i making the best prediction compared to other models in the set being considered.

Model weights summed together = 1

Monkies and Milk

data(milk)
d <- milk[ complete.cases(milk) , ]
d$neocortex <- d$neocortex.perc / 100

A lotta Models

a.start <- mean(d$kcal.per.g)
sigma.start <- log(sd(d$kcal.per.g))

#null
m6.11 <- map(
    alist(
        kcal.per.g ~ dnorm( a , exp(log.sigma) )
    ) ,
    data=d , start=list(a=a.start,log.sigma=sigma.start) )

#neocortex only
m6.12 <- map(
    alist(
        kcal.per.g ~ dnorm( mu , exp(log.sigma) ) ,
        mu <- a + bn*neocortex
    ) ,
    data=d , start=list(a=a.start,bn=0,log.sigma=sigma.start) )

A lotta Models

# log(mass) only
m6.13 <- map(
    alist(
        kcal.per.g ~ dnorm( mu , exp(log.sigma) ) ,
        mu <- a + bm*log(mass)
    ) ,
    data=d , start=list(a=a.start,bm=0,log.sigma=sigma.start) )

# neocortex + log(mass)
m6.14 <- map(
    alist(
        kcal.per.g ~ dnorm( mu , exp(log.sigma) ) ,
        mu <- a + bn*neocortex + bm*log(mass)
    ) ,
    data=d , start=list(a=a.start,bn=0,bm=0,log.sigma=sigma.start) )

A WAIC

WAIC( m6.14 )
       WAIC     lppd  penalty  std_err
1 -15.07116 12.33633 4.800753 7.684498

Comparing Models

milk.models <- compare( m6.11 , m6.12 , m6.13 , m6.14)
milk.models
            WAIC       SE    dWAIC      dSE    pWAIC     weight
m6.14 -14.531291 7.616650 0.000000       NA 5.083474 0.91135329
m6.13  -8.303929 5.532010 6.227362 5.342747 2.824969 0.04049788
m6.11  -8.027938 4.684037 6.503353 7.242885 1.943980 0.03527780
m6.12  -6.011389 4.285965 8.519902 7.511702 3.000938 0.01287103

Comparing Models

plot(milk.models, cex=1.5)
solid = deviance, circle=WAIC, triangle = \(\Delta\)WAIC

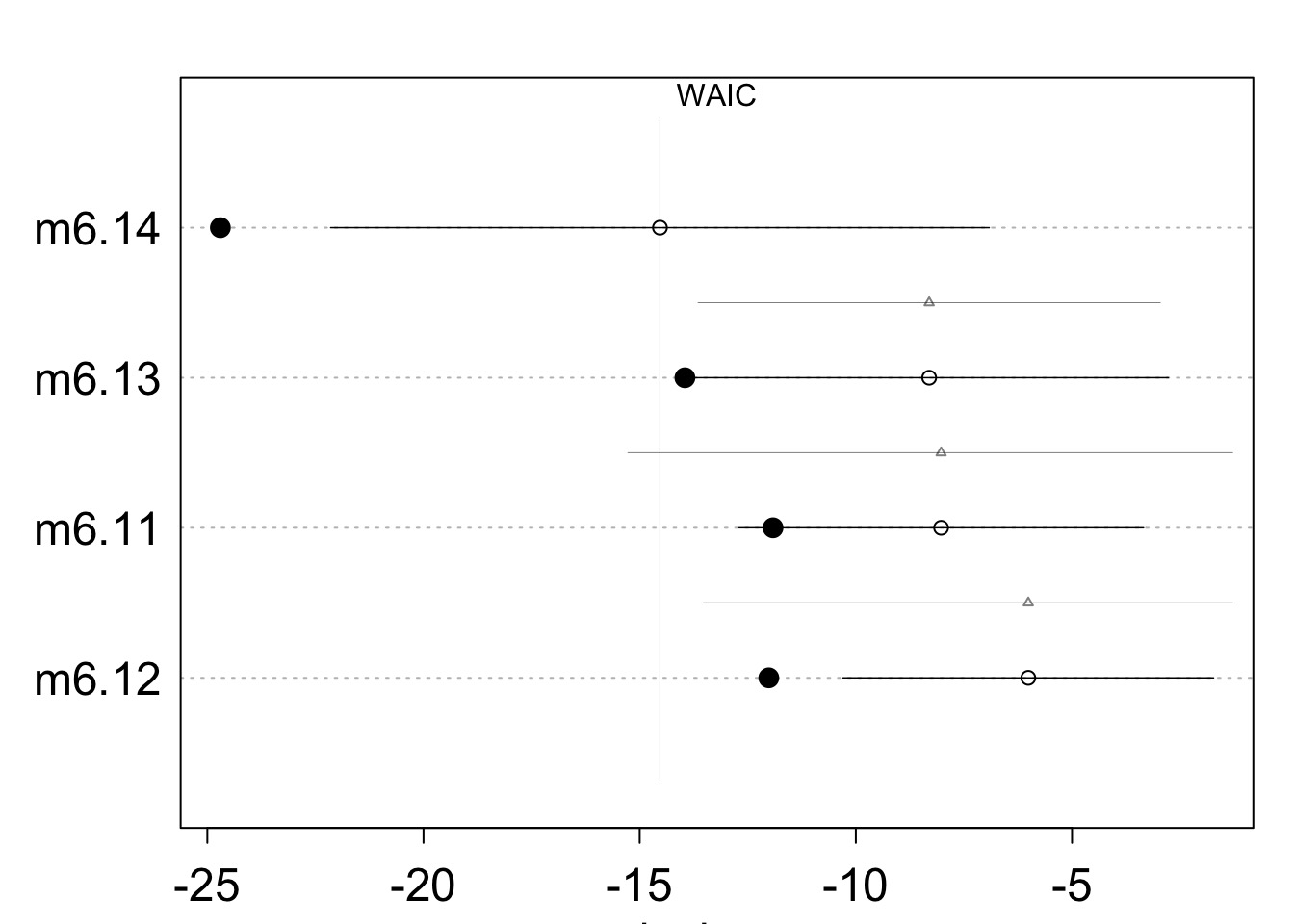
Comparing Models with PSIS

milk.models.psis <- compare( m6.11 , m6.12 , m6.13 , m6.14, func = PSIS)
plot(milk.models.psis)

PSIS and Warnings of Big Weights

       PSIS     lppd  penalty  std_err
1 -8.269555 4.134778 1.804511 4.573406

PSIS and Warnings of Big Weights

          PSIS        lppd    penalty  std_err           k
1  -0.54379033  0.27189516 0.07536975 4.918592 0.110928428
2  -0.25100413  0.12550207 0.09667641 4.918592 0.141064066
3  -1.28505873  0.64252937 0.03767753 4.918592 0.137201566
4   0.64800200 -0.32400100 0.21765862 4.918592 0.379834740
5   1.36161094 -0.68080547 0.32809924 4.918592 0.517833782
6  -0.83764796  0.41882398 0.05905439 4.918592 0.293044647
7  -0.08966115  0.04483057 0.11008533 4.918592 0.132774264
8  -1.54312140  0.77156070 0.02701942 4.918592 0.057620921
9  -1.63104150  0.81552075 0.02591626 4.918592 0.113083685
10  2.88287292 -1.44143646 0.62759197 4.918592 0.863425023
11 -0.28576746  0.14288373 0.10560214 4.918592 0.196157674
12 -1.59790928  0.79895464 0.02837054 4.918592 0.009027069
13 -1.11645979  0.55822989 0.04407620 4.918592 0.193489797
14 -0.54379033  0.27189516 0.07536975 4.918592 0.110928428
15 -0.40187958  0.20093979 0.08537474 4.918592 0.095956746
16 -1.20492392  0.60246196 0.04056094 4.918592 0.195238557
17 -1.54312140  0.77156070 0.02701942 4.918592 0.057620921

Using WAIC and PSIS to Determine Problem Points

[1] "M mulatta"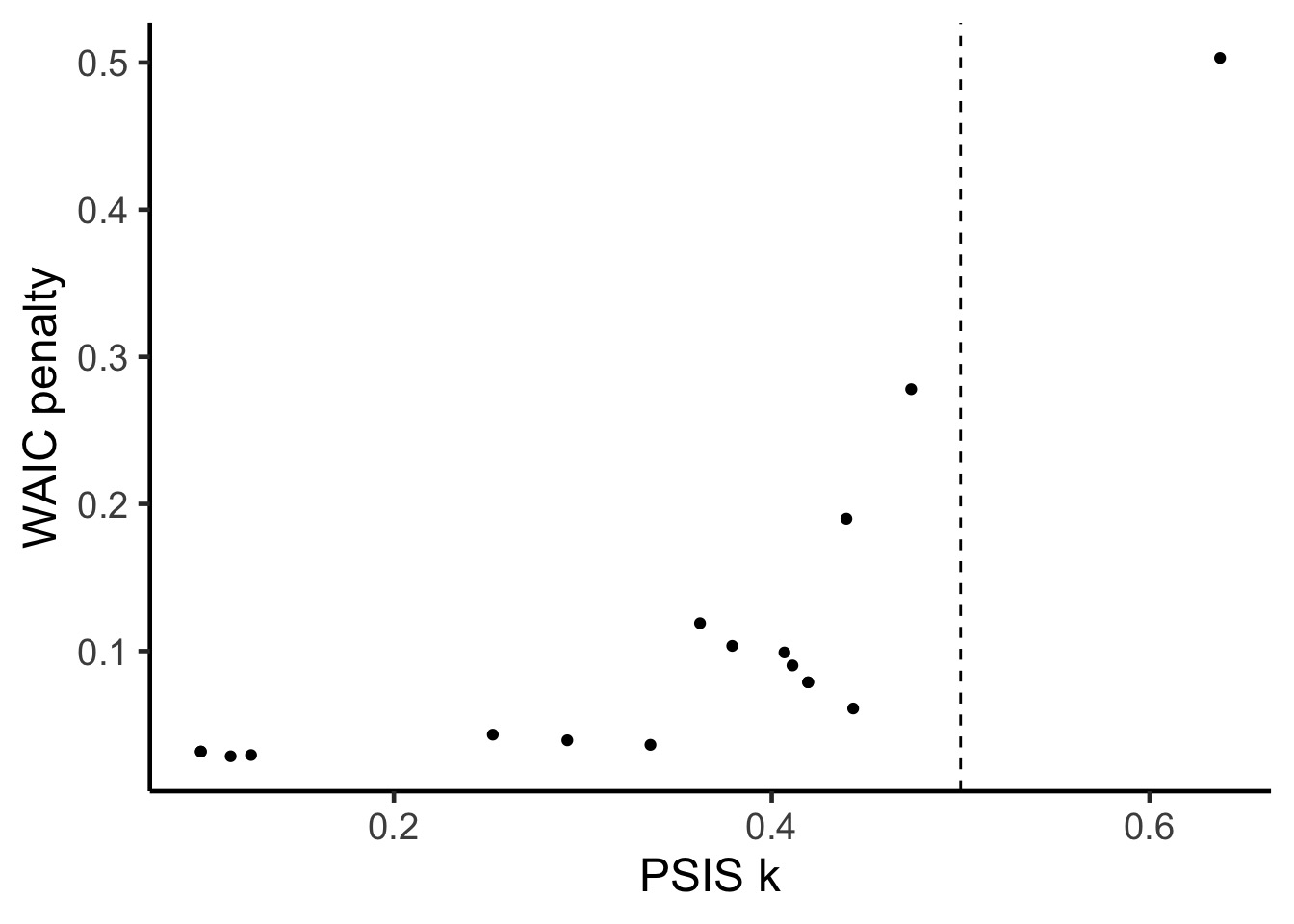

Death to model selection

  • While sometimes the model you should use is clear, more often it is not

  • Further, you made those models for a reason: you suspect those terms are important

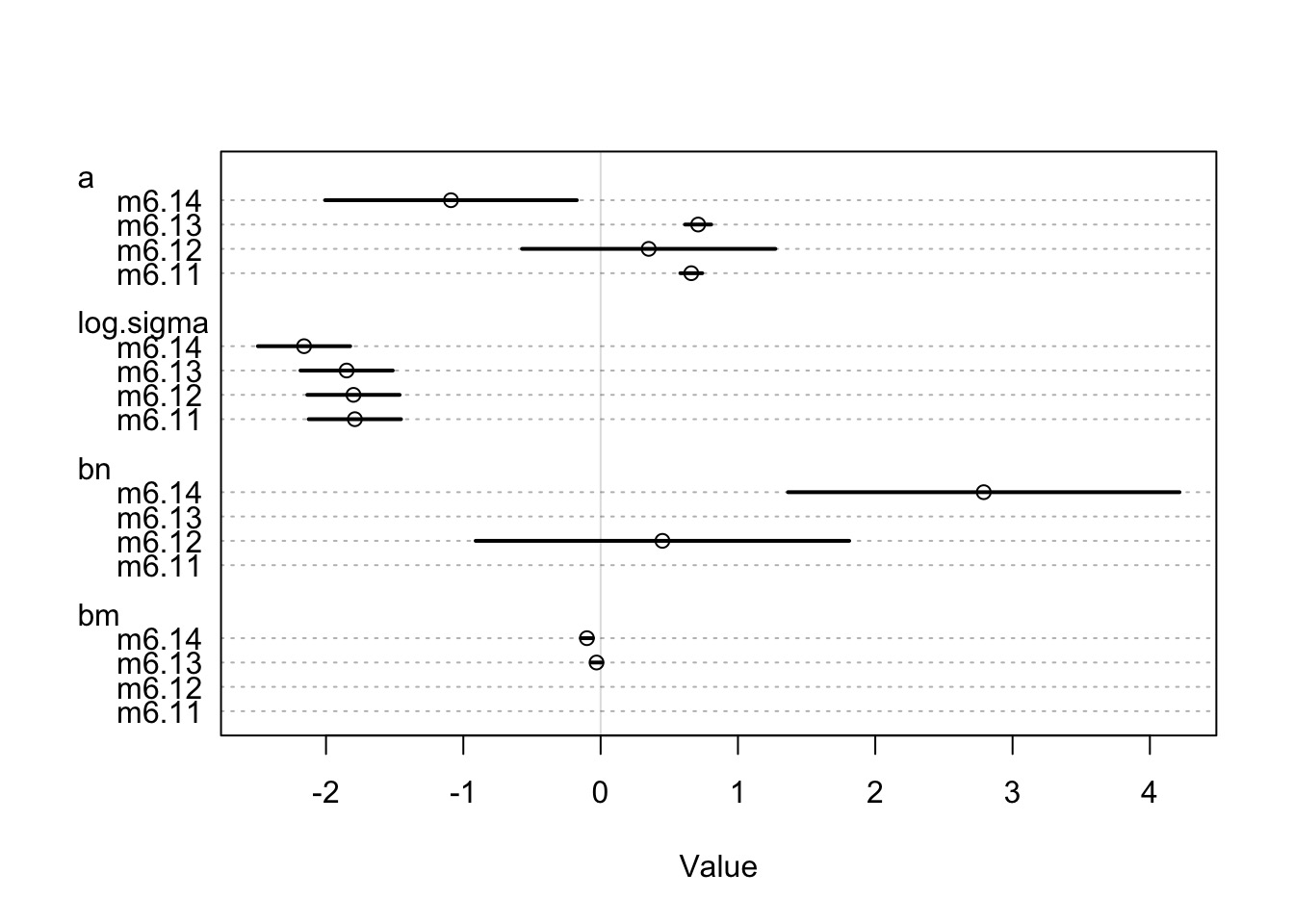
  • Better to look at coefficients across models

  • For actual predictions, ensemble predictions provide real uncertainty

Coefficients

Remember, m6.14 has a 97% WAIC model weight

ctab <- coeftab( m6.11 , m6.12 , m6.13 , m6.14)
ctab
          m6.11   m6.12   m6.13   m6.14  
a            0.66    0.35    0.71   -1.09
log.sigma   -1.79   -1.80   -1.85   -2.16
bn             NA    0.45      NA    2.79
bm             NA      NA   -0.03   -0.10
nobs           17      17      17      17

Coefficients

Remember, m6.14 has a 97% WAIC model weight

plot(ctab)

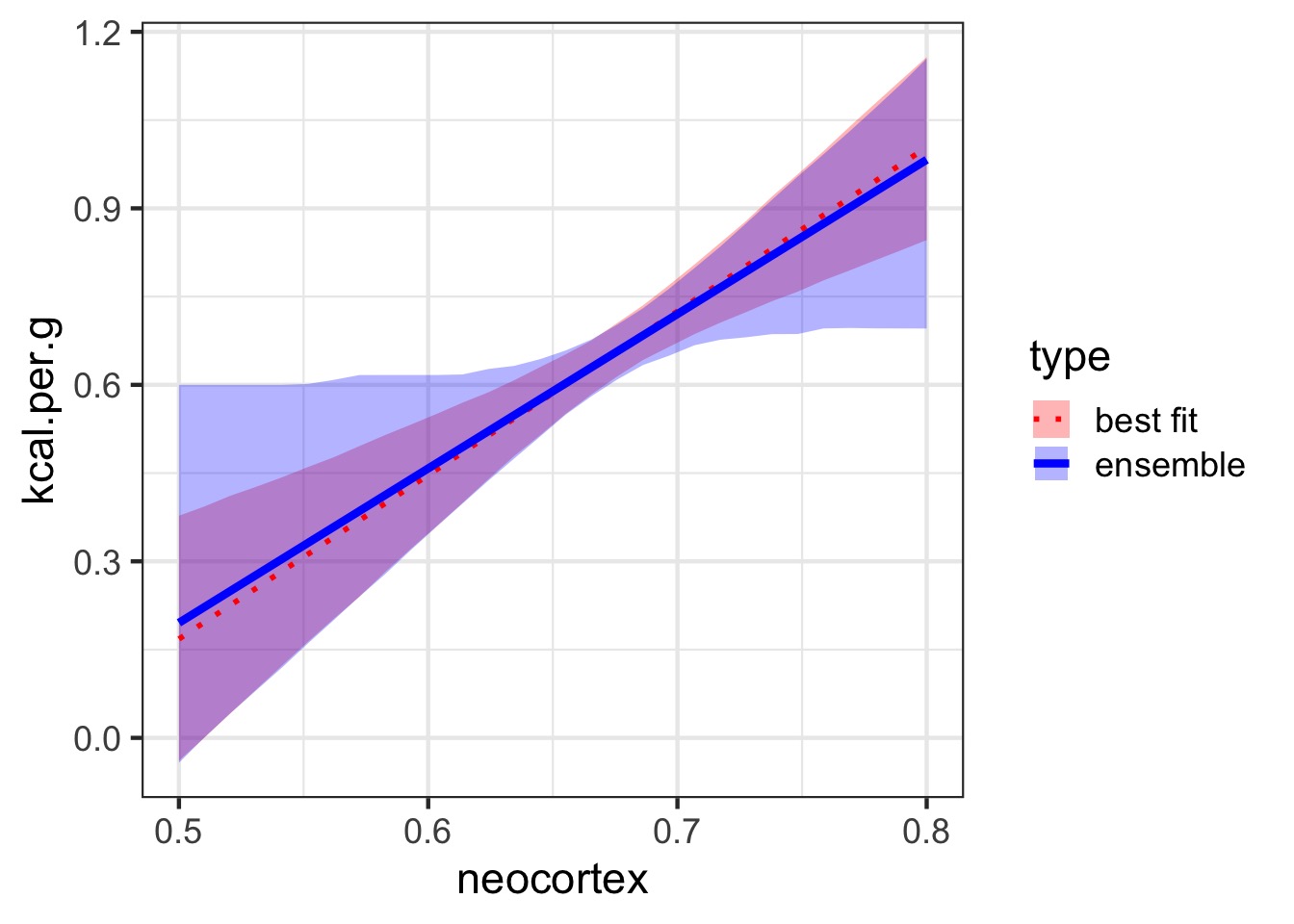
Ensemble Prediction

  • Ensemble prediction gives us better uncertainty estimates

  • Takes relative weights of predictions into account

  • Takes weights of coefficients into account

  • Basicaly, get simulated predicted values, multiply them by model weight

Making an Ensemble

# data for prediction
nc.seq <- seq(from=0.5,to=0.8,length.out=30)

d.predict <- data.frame(
    kcal.per.g = rep(0,30), # empty outcome
    neocortex = nc.seq,     # sequence of neocortex
    mass = rep(4.5,30)      # average mass
)

# make the ensemble
milk.ensemble <- ensemble( m6.11, m6.12, 
                           m6.13 ,m6.14 , data=d.predict )

# get 
mu_ensemble <- apply( milk.ensemble$link , 2 , mean )
mu.PI_fit <- apply( milk.ensemble$link , 2 , PI )

Making an Ensemble

Exercise

  • Take your milk multiple predictor models with clade, milk components, both, and neither

  • Compare via WAIC

  • Get ensemble predictions for each clade