22_varying_intercept.utf8.md

Bayesian Approaches to Mixed (aka Hierarchical, aka Multilevel) Models

Mixed Models

We have used these to tease out variation in parameters due to “blocks”
Many kinds of “blocks”
Variation can affect slopes and intercepts
Variation can come from continuous “blocks” - Gaussian Process Models
But what do we gain?

Gains from a Mixed Model Approach

Shrinkage of Estimators
Accurate post-hoc comparisons
Better ability to make focused predictions

The Incredible Shrinking Frogs

The Reed Frog Data

library(rethinking)
data(reedfrogs)
head(reedfrogs)

  density pred  size surv propsurv
1      10   no   big    9      0.9
2      10   no   big   10      1.0
3      10   no   big    7      0.7
4      10   no   big   10      1.0
5      10   no small    9      0.9
6      10   no small    9      0.9

Tank as a block

48 tanks
Each tank has different number of frogs
Each frog is a “replicate”
- 1/0 live/die
Each tank is a “block”

reedfrogs$tank <- 1:nrow(reedfrogs)

Three ways of looking at survivorship

1. Every tank has the same survivorship (complete pooling)

2. Every tank has its own unique survivorship (no pooling)

3. Every tank is similar to others, but with some variation in survivorship (partial pooling)

Complete Pooling

mod_fullpool <- alist(
  
  #likelihood
  surv ~ dbinom(density, prob),
  
  #Data Generating Process
  logit(prob) <- p,
  
  #Priors
  p ~ dnorm(0,10)
)

fit_fullpool <- map2stan(mod_fullpool, data=reedfrogs)

Estimates mean probability across all tanks

No Pooling

mod_nopool <- alist(
  
  #likelihood
  surv ~ dbinom(density, prob),
  
  #Data Generating Process
  logit(prob) <- p[tank],
  
  #Priors
  p[tank] ~ dnorm(0,10)
)

fit_nopool <- map2stan(mod_nopool, data=reedfrogs)

Each tank is independent

Partial Pooling and Hyperparameters

p[tank] ~ dnorm(0,10)

P[tank] can be anything, and our prior for p[tank] shows a distribution of possible values

But now…
p[tank] ~ dnorm(p_hat, sigma_tank)

P[tank] is drawn from a distribution, and p_hat and sigma_tank are hyperparameters, each with their own prior

This can go on forever…

Partial Pooling

mod_partialpool <- alist(
  
  #likelihood
  surv ~ dbinom(density, prob),
  
  #DGP
  logit(prob) <- p[tank],
  
  #Define random effects (part of DGP!)
  p[tank] ~ dnorm(p_hat, sigma_tank),

  #Priors
  p_hat ~ dnorm(0,10),
  sigma_tank ~ dcauchy(0,2)
)

fit <- map2stan(mod_partialpool, data=reedfrogs)

\[p_j \sim dnorm(\widehat{p} , \sigma_{tank})\]

The Mathy Version

Likelihood
\(Survivors_j \sim dbinom(density_j , prob_j)\)

Data Generating Process
\(logit(prob_j) = p_j\)

\(p_j \sim dnorm(\widehat{p} , \sigma_{tank})\)

Priors
\(\widehat{p} \sim dnorm(0,10)\)
\(\sigma_{tank} \sim dcauchy(0,2)\)

Why Partial Pooling?

Share information across blocks
- estimate of one block informs the other
- super helpful with unbalanced designs
- Enables Best Least Unbiased Predictor (BLUP) of observations
Reduces number of effective parameters
Improved estimation of true underlying parameter
- Observed values have additional error, reduces accuracy

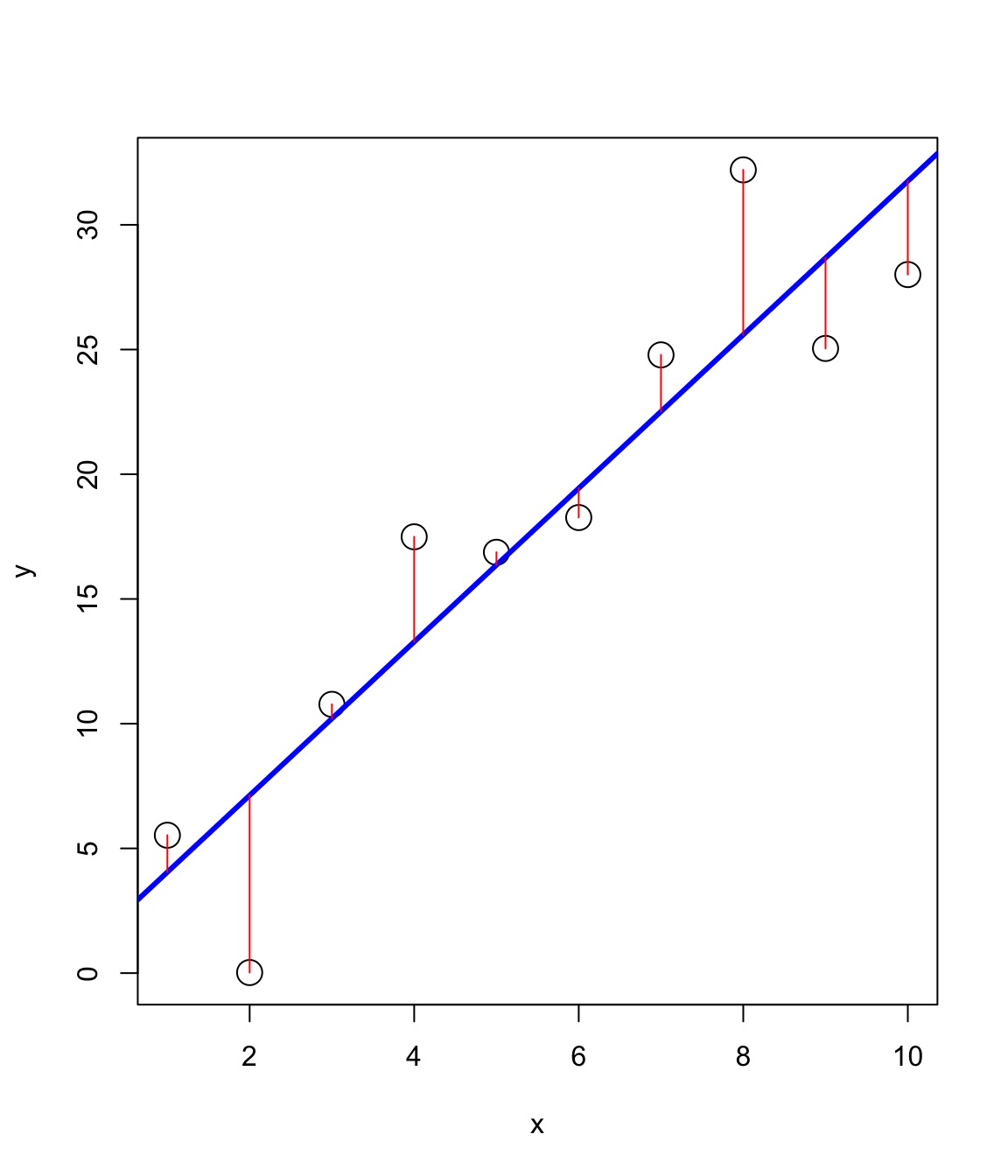
Shrinkage in Frog Survivorship

Shrinkage and Unbalanced Designs

Partial Pooling Better for Unbalanced Designs

Comparing Approaches

compare(fit, fit_nopool, fit_fullpool)

               WAIC pWAIC dWAIC weight    SE   dSE
fit          1011.1  38.5   0.0      1 38.15    NA
fit_nopool   1027.7  52.4  16.6      0 44.40  8.58
fit_fullpool 1372.0   1.0 360.9      0 25.87 35.12

Improved fit from partial pooling
Big reduction in number of parameters
- From reducing paramter variance (remember pWAIC definition!)

Reduced Parameter Variance

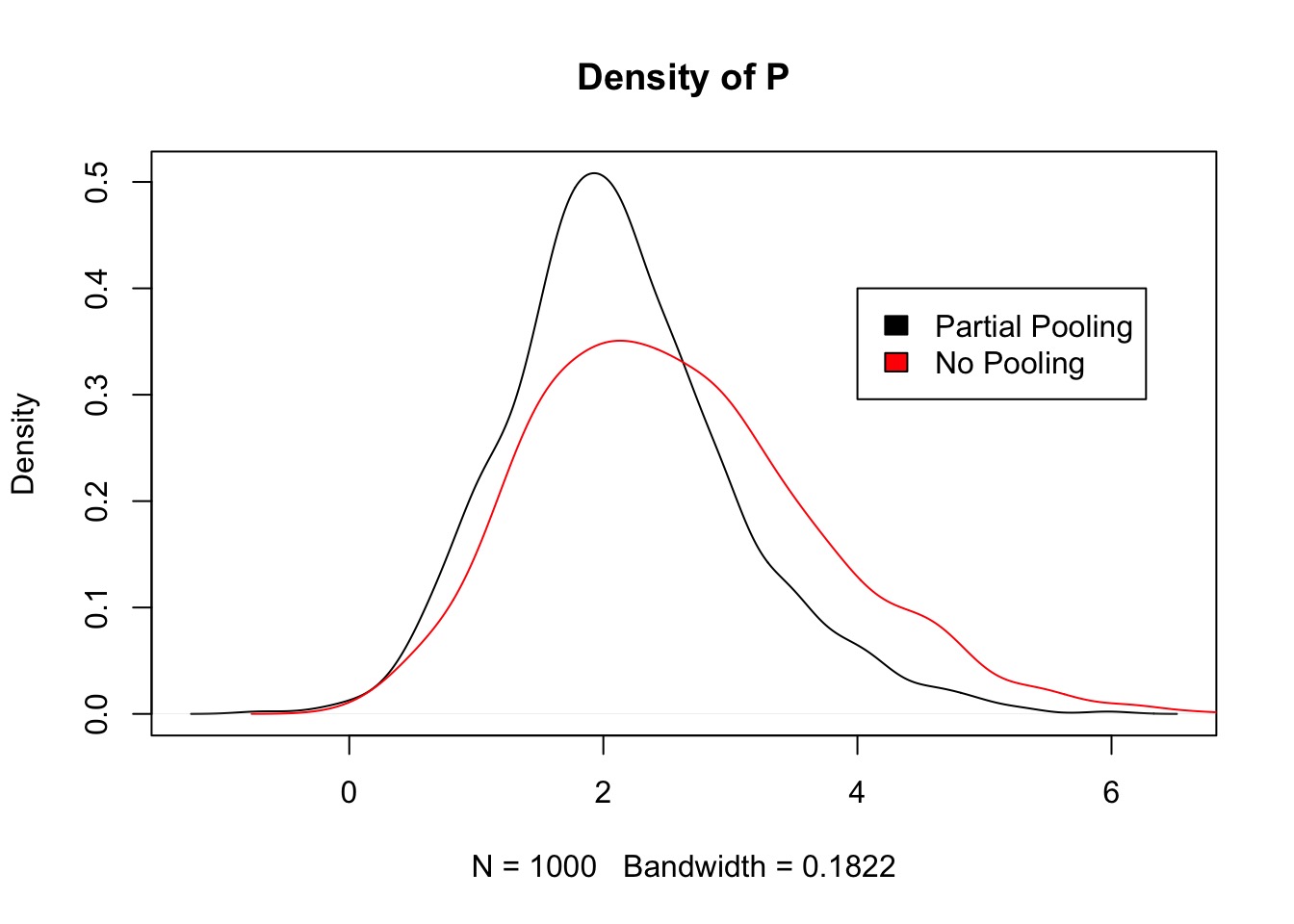
Fit and Overdispersion

Overdispersed models are kinda mixed models already
- Parameters of distribution vary with their own distribution
- We use a formal compound distribution, but the concept is the same
Mixed models have coefficients vary by distribution
- Variation injected earlier, but similar effect

Oceanic Tool Use

     culture population contact total_tools mean_TU
1   Malekula       1100     low          13     3.2
2    Tikopia       1500     low          22     4.7
3 Santa Cruz       3600     low          24     4.0
4        Yap       4791    high          43     5.0
5   Lau Fiji       7400    high          33     5.0
6  Trobriand       8000    high          19     4.0

A Typical Model

Kline$log_pop <- log(Kline$population)

kline_mod <- alist(
  #Likelihood
  total_tools ~ dpois(lambda),
  
  #DGP
  log(lambda) ~ a + bp*log_pop,
  
  #Priors
  a ~ dnorm(0,10),
  bp ~ dnorm(0,1)
)

kline_fit <- map(kline_mod, data=Kline)

Overdispersion?

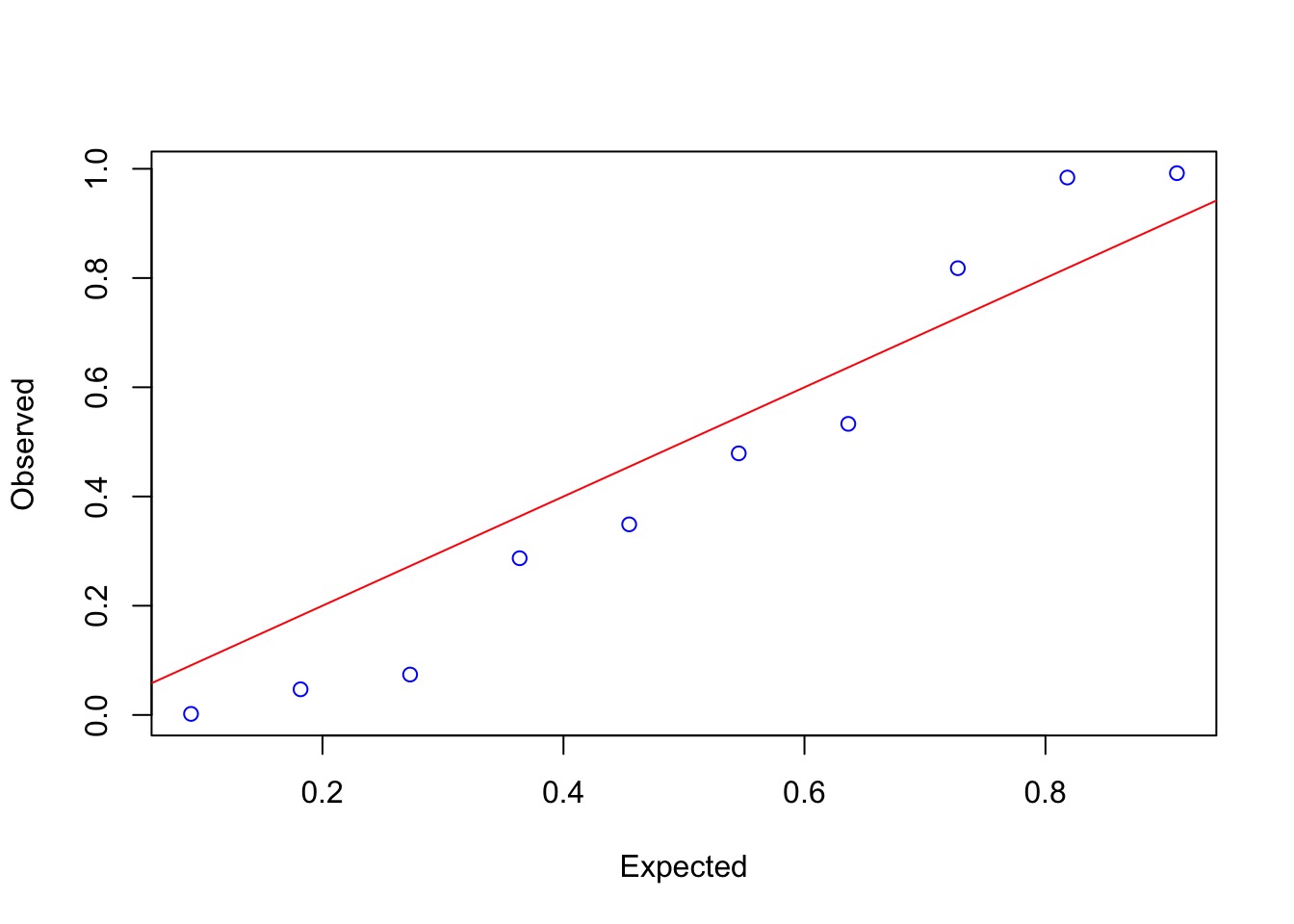
Mild, but yes.

An Overdispersed Model

Kline$log_pop <- log(Kline$population)

kline_over <- alist(
  #Likelihood
  total_tools ~ dgampois(lambda, scale),
  
  #DGP
  log(lambda) ~ a + bp*log_pop,
  
  #Priors
  a ~ dnorm(0,10),
  bp ~ dnorm(0,1),
  scale ~ dexp(2)
)

kline_over_fit <- map2stan(kline_over, data=Kline)

Overdispersion needed

      Mean StdDev lower 0.89 upper 0.89 n_eff Rhat
a     0.98   1.57      -1.58       3.22   291 1.00
bp    0.28   0.17       0.01       0.54   297 1.00
scale 2.22   0.94       0.86       3.57   356 1.01

Overdispersion helps

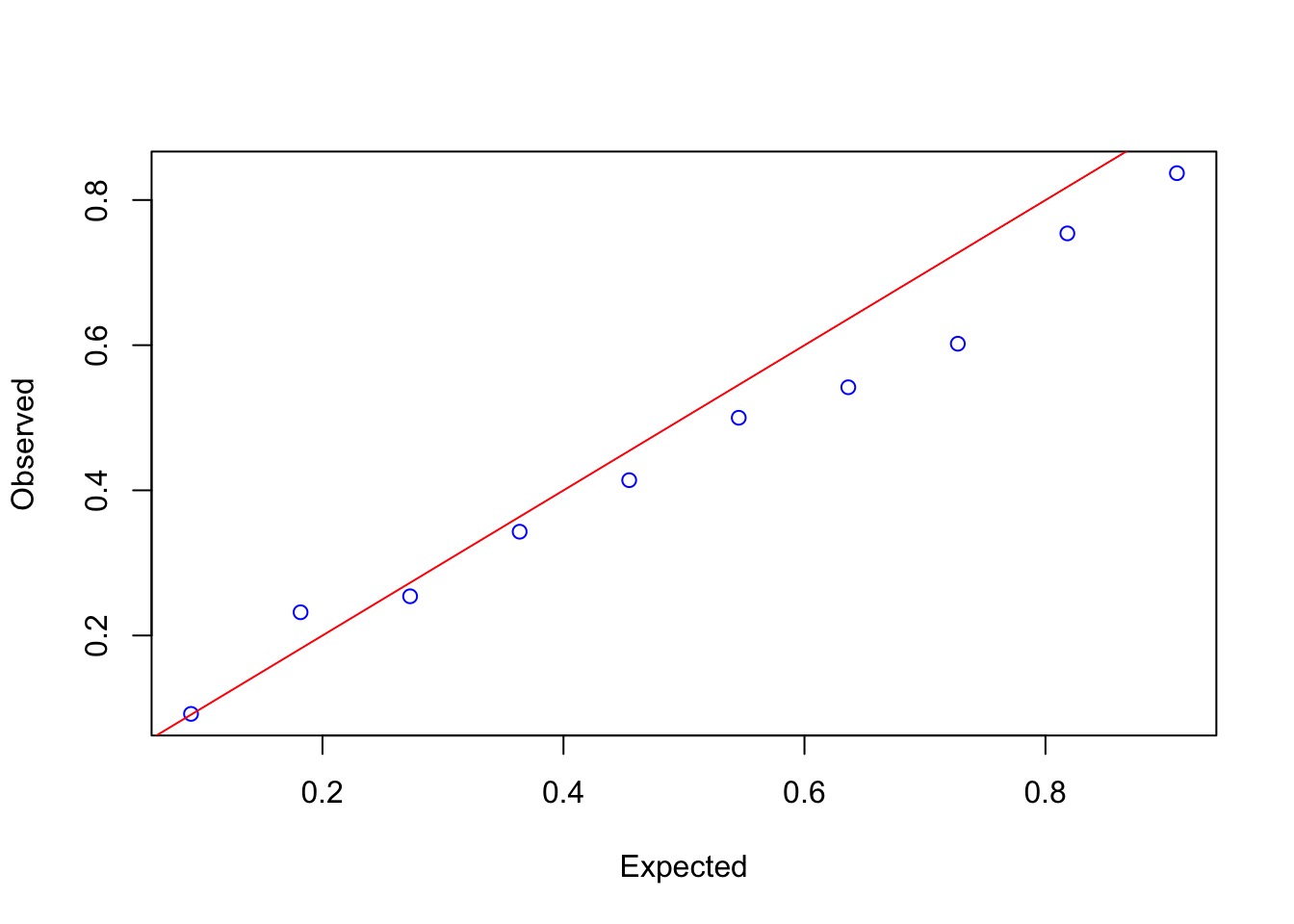
What about modeling random variation in societies?

Kline$society <- 1:nrow(Kline)

kline_mixed <- alist(
  #Likelihood
  total_tools ~ dpois(lambda),
  
  #DGP
  log(lambda) ~ a[society] + bp*log_pop,
  
  a[society] ~ dnorm(a_hat, sigma_society),

  #Priors
  a_hat ~ dnorm(0,10),
  bp ~ dnorm(0,1),
  sigma_society ~ dcauchy(0,2)
)

kline_mixed_fit <- map2stan(kline_mixed, data=Kline,
                            iter=10000, chains=3)

Overdispersion Handled Here, Too

Exercise

Revisit the Reed Frog survivorship
Fit models with 1) predation and frog size acting additively, 2) both interacting, and 3) a null model.
- All should have tank as a random effect.
Feel free to try with lme4 first just to get your bearings
Compare all three with WAIC
How does sigma_tank change across the different models?