Markov Chain Monte Carlo

Our Story Thus Far…
- We have been using Maximum A Posteriori Approximations
- Assumes Gaussian posterior (approximately quadratic)
- Great for simple models
But…
- We’ve noticed problems with models of moderate complexity
- Many problems do not have easy analytical solution
- Autocorrelation
- State-Space Models
- Mixed Models
- Autocorrelation
- Solution is simulated draws form the posterior…
King Markov and His Islands

King Markov and His Islands


How to move around Islands

What Metropolis MCMC Looks Like
mcmc_ex <- function(num_weeks = 1e5, current=10, positions = rep(0, num_weeks)){
for ( i in 1:num_weeks ) {
# record current position
positions[i] <- current
# flip coin to generate proposal
proposal <- current + sample( c(-1,1) , size=1 )
# now make sure he loops around the archipelago
if ( proposal < 1 ) proposal <- 10
if ( proposal > 10 ) proposal <- 1
# move?
prob_move <- proposal/current
current <- ifelse( runif(1) < prob_move , proposal , current )
}
positions
}Metropolis MCMC in Action: 10 Weeks
Population = Island Number 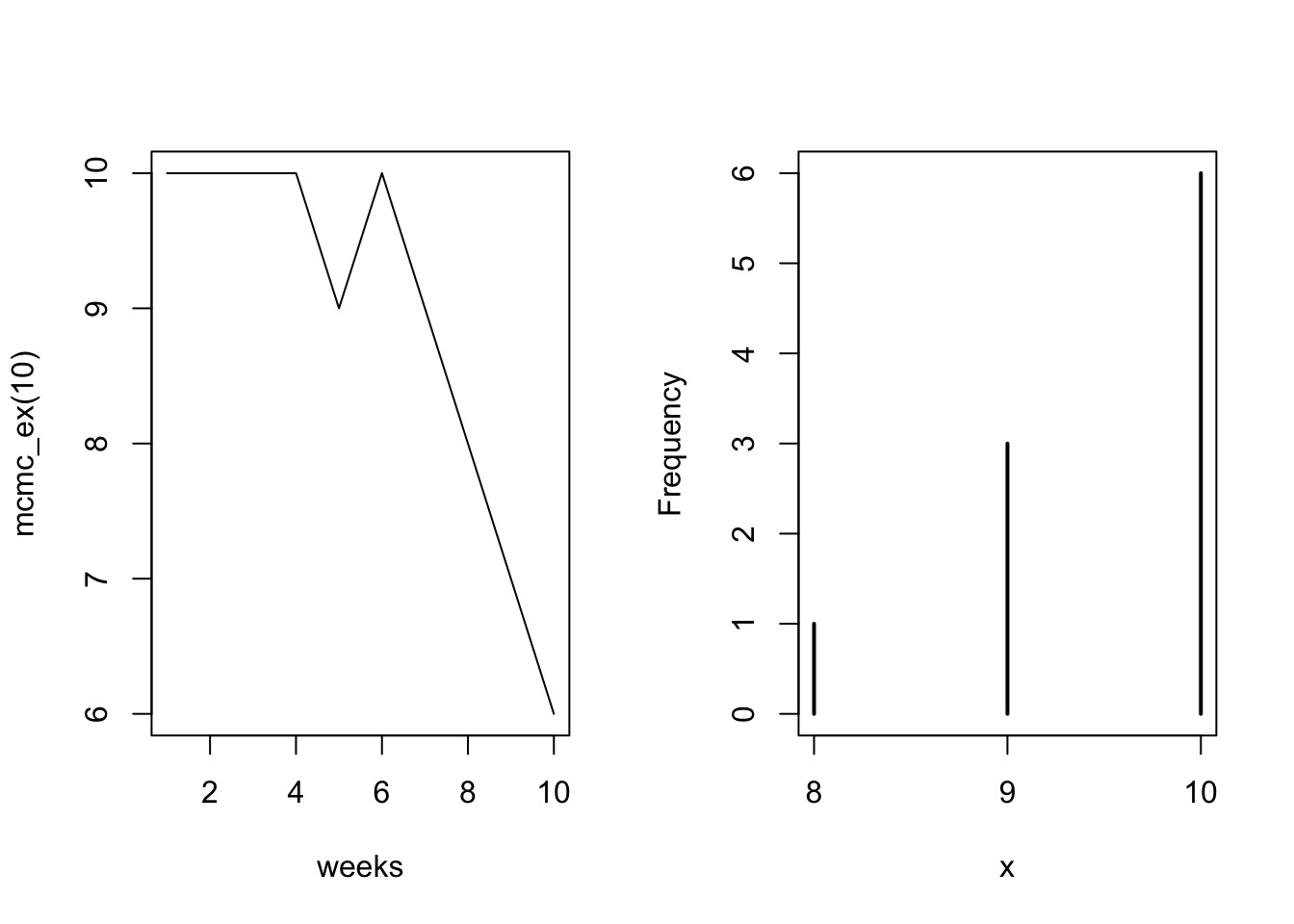
Metropolis MCMC in Action: 50 Weeks
Population = Island Number 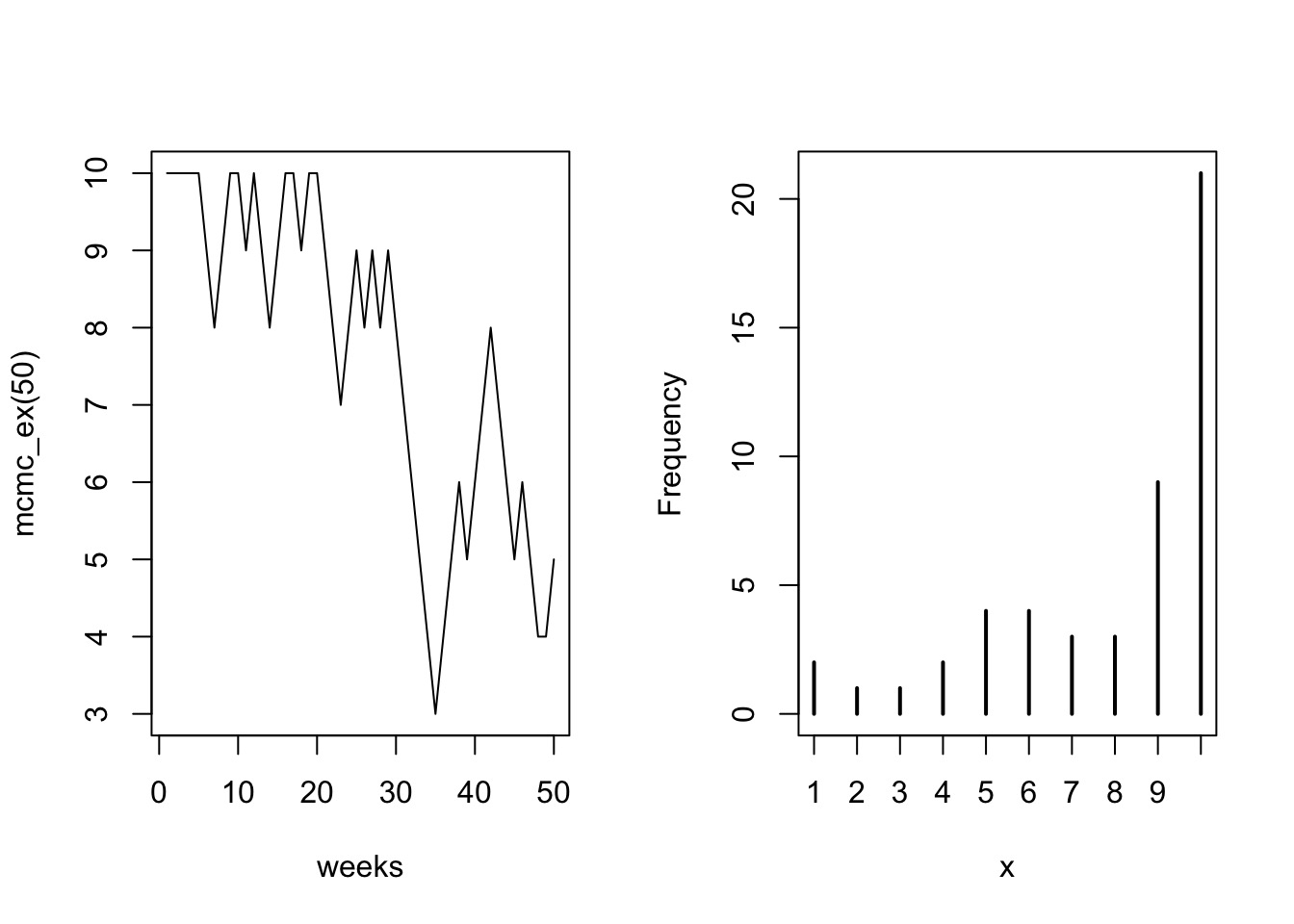
Metropolis MCMC in Action: 1000 Weeks
Population = Island Number 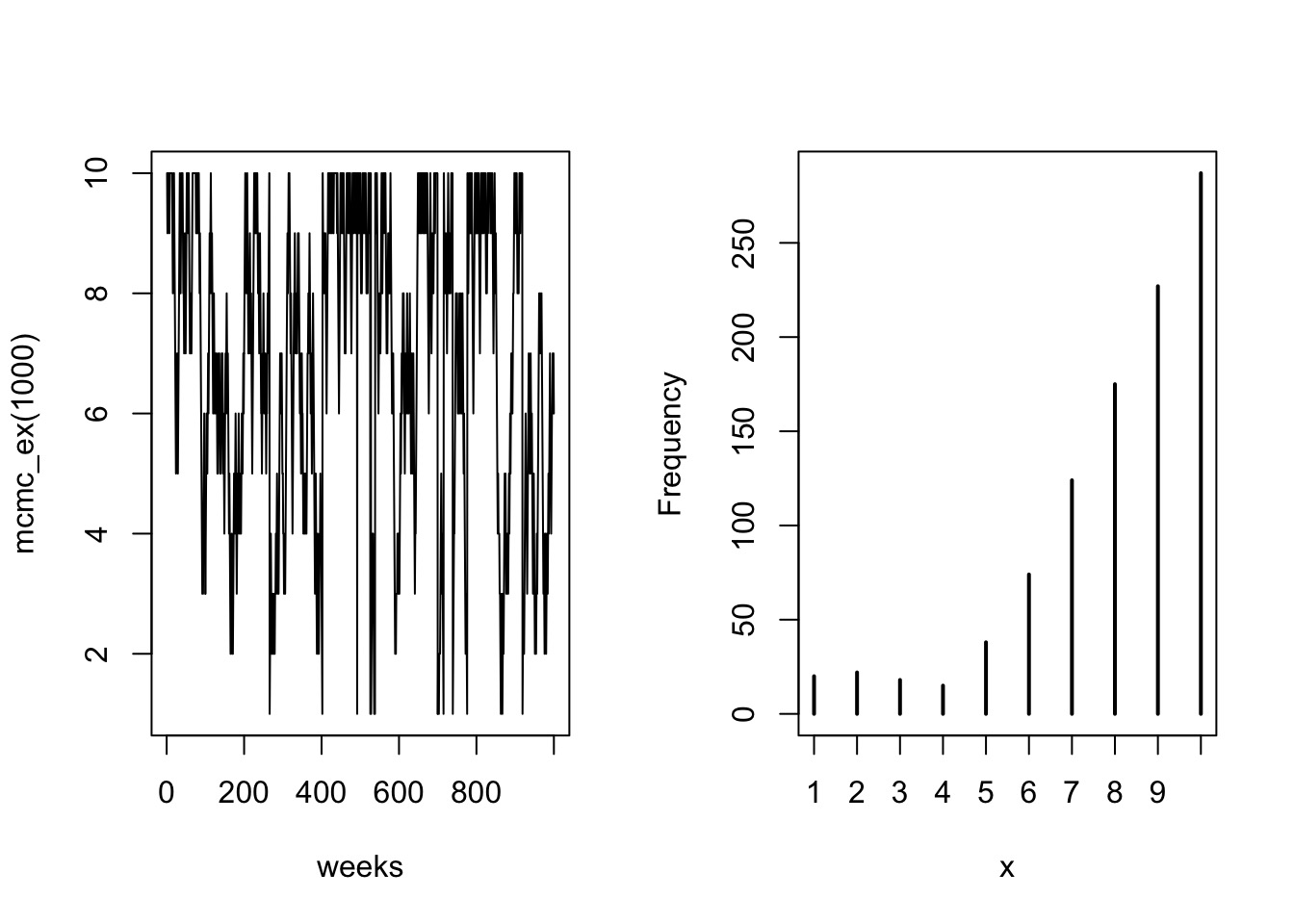
Metropolis MCMC For Models
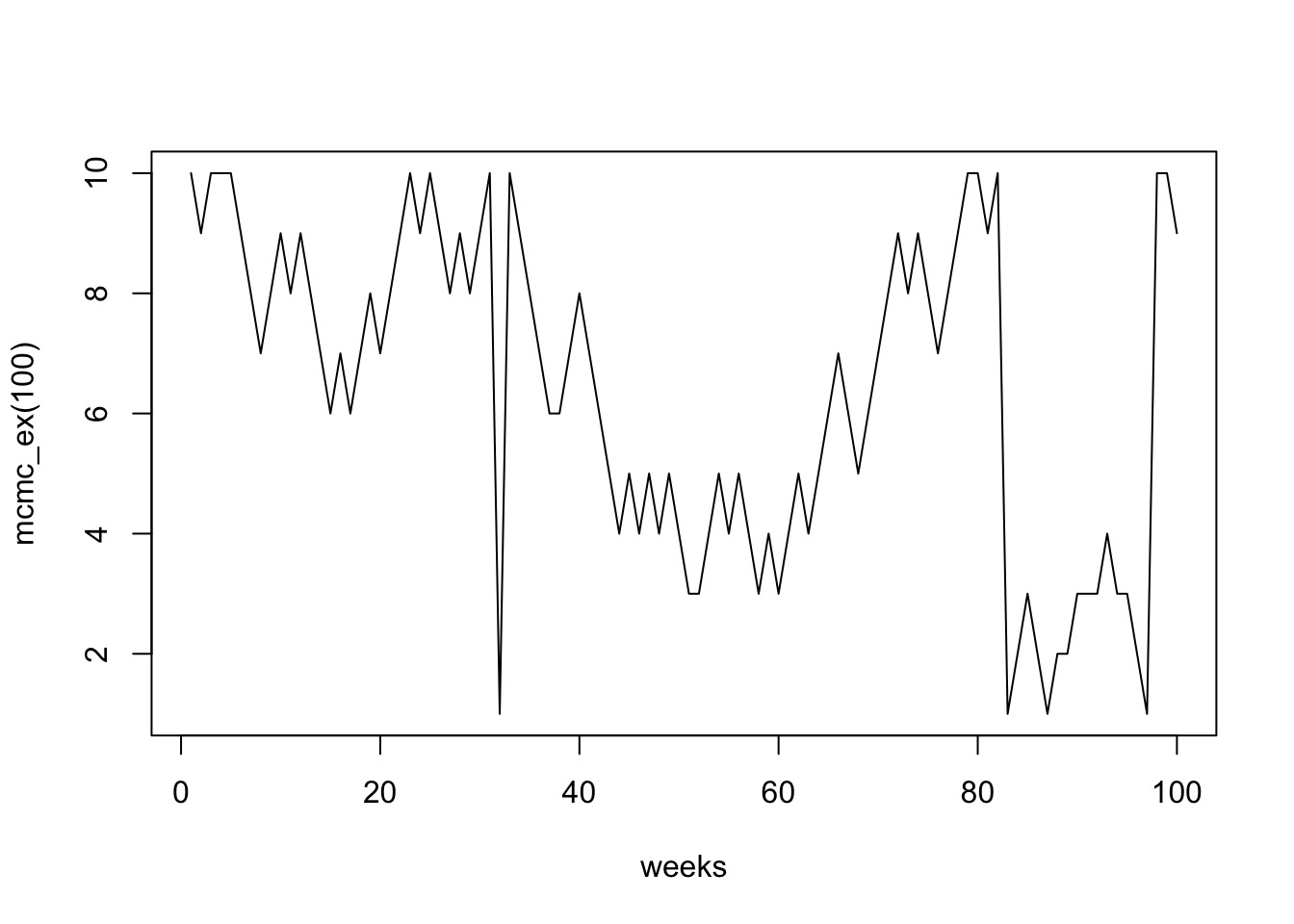
- Each island is a set of parameter choices
- Each “population” is a posterior density
- The path is a ‘chain’
- Note the autocorrelation - we “thin” chains
- Only use every ith sample so that there is no autocorrelation
MCMC In Practice for Models
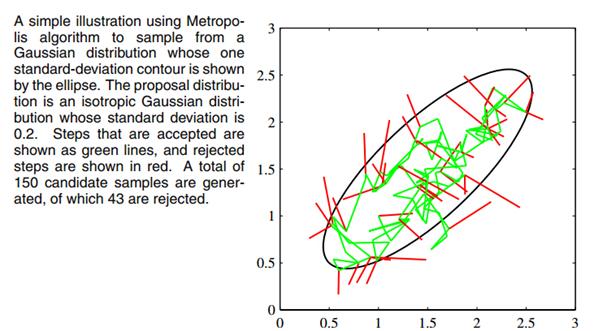
MCMC is not a Panacea

MCMC is not a Panacea
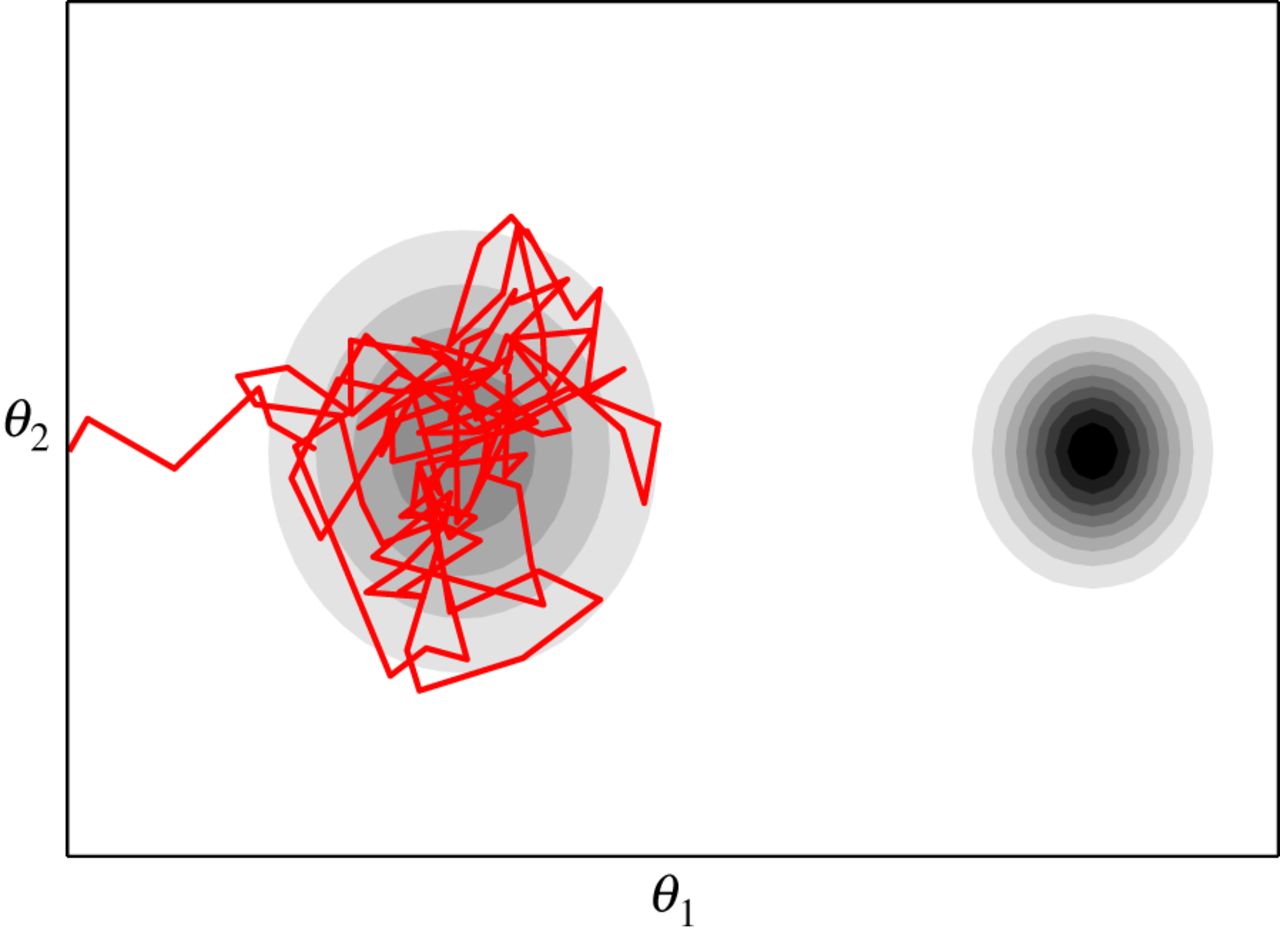
How can MCMC Fail?
- MCMC (particularly Metropolis) can get stuck
- Start values can still be important
- Particularly a problem with many parameters which are correlated
- One way we try and assess is fit with many chains and make sure they converge
MCMC Algorithms
- Metropolis MCMC inefficient
- Many algorithms to come up with clever proposed moves to speed up
- Gibbs sampling used for BUGS, JAGS, etc.
- Still has same problems as Metropilis
- Or… Abandon search and use more deterministic sampling
- Hamiltonian MCMC

King Hamilton and His BatBoat


King Hamilton and His BatBoat

- Boat passes by all of the island, back and forth
- Boat slows down to see people in porportion to how many folk
- We sample position through time, more positions in areas where boat is slow
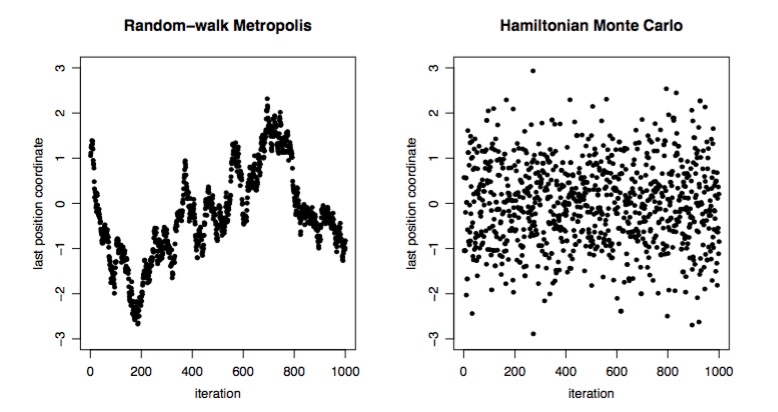
Metropolis versus Hamiltonian
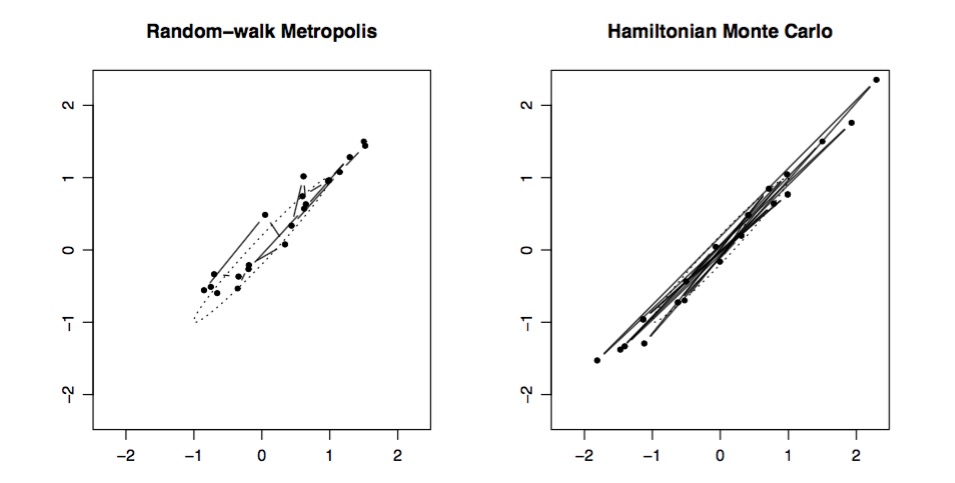
Metropolis versus Hamiltonian
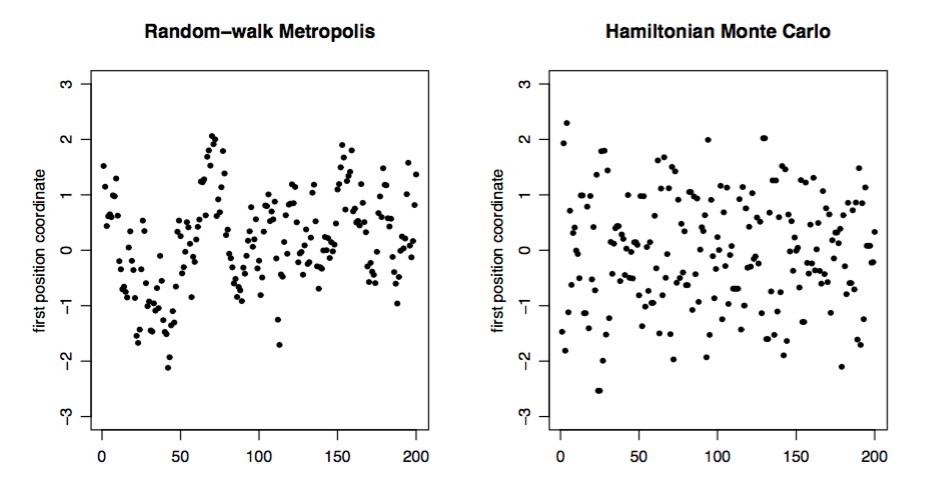
Metropolis versus Hamiltonian
Implementing HMCMC via Stan

- We use the
map2stanfunction to call STAN- Compiles a model, so it can take a while
- Compiles a model, so it can take a while
- Can specify number of chains and other parameters
- And now our samples are already part of our model!
- Careful, models can get large (in size) depending on number of parameters and samples
Data Prep for HMCMC
data(rugged)
rugged$log_gdp <- log(rugged$rgdppc_2000)
#Prep the data
d <- rugged[complete.cases(rugged$log_gdp),]
# Need indices >0
d$cont_africa <- d$cont_africa +1
# Only want the data we are using
# (otherwise slows STAN down)
d.trim <- d[ , c("log_gdp","rugged","cont_africa") ]The Model…
int_mod <- alist(
#likelihood
log_gdp ~ dnorm(mu, sigma),
#Data generating process
mu <- bR[cont_africa]*rugged + bA[cont_africa],
#priors
bR[cont_africa] ~ dnorm(0,1),
bA[cont_africa] ~ dnorm(8,100),
sigma ~ dcauchy(0,2)
)
Wait, Cauchy???
Sidenote: the Cauchy Distribution
- Pronounced Ko-she
- A ratio of two normal distributions
- Large thick tail
- Extreme values regularly sampled
- Uses half-cauchy, so, only positive

Fitting with map2stan
fit <- map2stan(int_mod, data=d.trim)warning: unknown warning option '-Wno-nneeded-internal-declaration'; did you mean '-Wno-unneeded-internal-declaration'? [-Wunknown-warning-option]
In file included from file111646090ffe9.cpp:8:
In file included from /Users/jearbear/Library/R/3.3/library/StanHeaders/include/src/stan/model/model_header.hpp:4:
In file included from /Users/jearbear/Library/R/3.3/library/StanHeaders/include/stan/math.hpp:4:
In file included from /Users/jearbear/Library/R/3.3/library/StanHeaders/include/stan/math/rev/mat.hpp:4:
In file included from /Users/jearbear/Library/R/3.3/library/StanHeaders/include/stan/math/rev/core.hpp:12:
In file included from /Users/jearbear/Library/R/3.3/library/StanHeaders/include/stan/math/rev/core/gevv_vvv_vari.hpp:5:
In file included from /Users/jearbear/Library/R/3.3/library/StanHeaders/include/stan/math/rev/core/var.hpp:7:
In file included from /Users/jearbear/Library/R/3.3/library/BH/include/boost/math/tools/config.hpp:13:
In file included from /Users/jearbear/Library/R/3.3/library/BH/include/boost/config.hpp:39:
/Users/jearbear/Library/R/3.3/library/BH/include/boost/config/compiler/clang.hpp:196:11: warning: 'BOOST_NO_CXX11_RVALUE_REFERENCES' macro redefined [-Wmacro-redefined]
# define BOOST_NO_CXX11_RVALUE_REFERENCES
^
<command line>:6:9: note: previous definition is here
#define BOOST_NO_CXX11_RVALUE_REFERENCES 1
^
2 warnings generated.
SAMPLING FOR MODEL 'log_gdp ~ dnorm(mu, sigma)' NOW (CHAIN 1).
Chain 1, Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1, Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1, Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1, Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1, Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1, Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1, Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1, Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1, Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1, Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1, Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1, Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.121338 seconds (Warm-up)
0.103927 seconds (Sampling)
0.225265 seconds (Total)
SAMPLING FOR MODEL 'log_gdp ~ dnorm(mu, sigma)' NOW (CHAIN 1).
WARNING: No variance estimation is
performed for num_warmup < 20
Chain 1, Iteration: 1 / 1 [100%] (Sampling)
Elapsed Time: 3e-06 seconds (Warm-up)
4.7e-05 seconds (Sampling)
5e-05 seconds (Total)
[ 100 / 1000 ]
[ 200 / 1000 ]
[ 300 / 1000 ]
[ 400 / 1000 ]
[ 500 / 1000 ]
[ 600 / 1000 ]
[ 700 / 1000 ]
[ 800 / 1000 ]
[ 900 / 1000 ]
[ 1000 / 1000 ]- Note where errors occur
- Warmup only?
- How often in your chain?
- Warmup only?
Inspect your Chains for convergence!
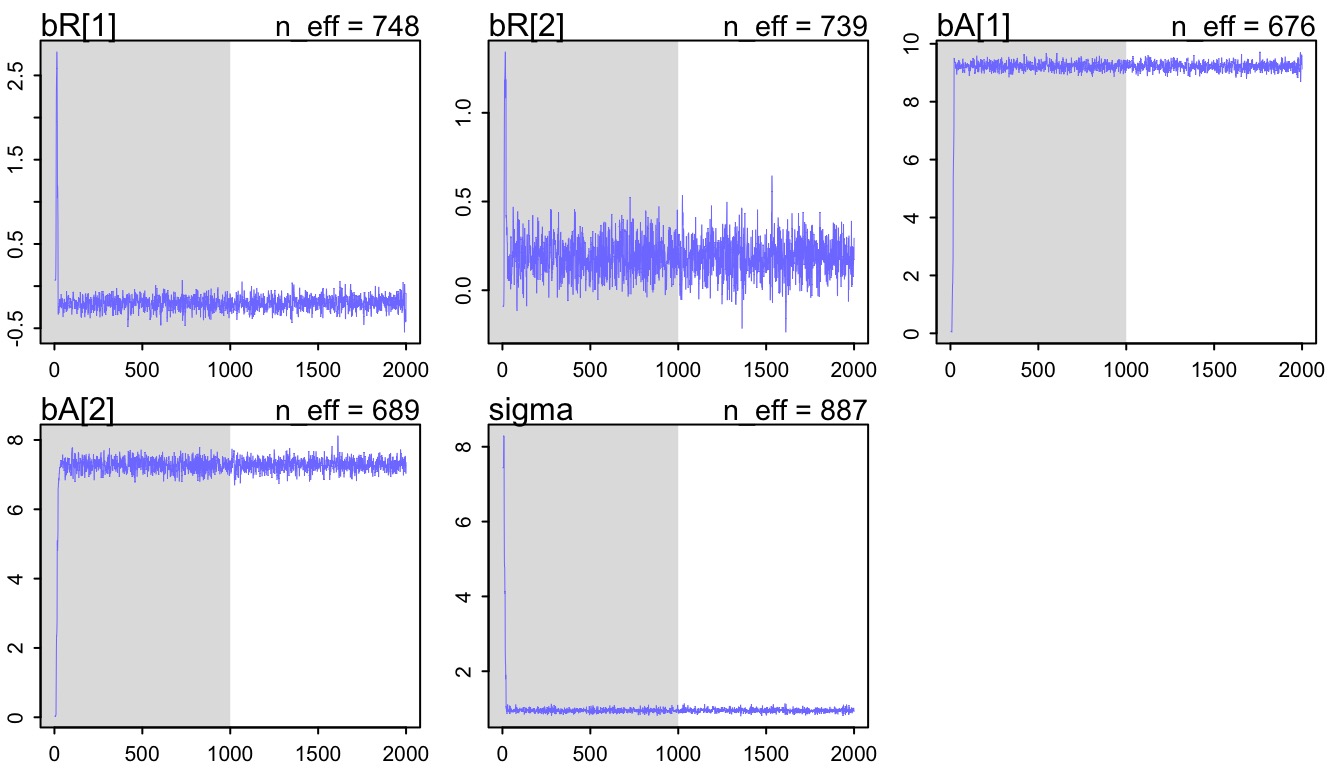
- Note, grey area is “warmup”
- Warmup is the BatBoat motoring around, tuning up
- Not used for posterior
- Warmup is the BatBoat motoring around, tuning up
Multiple Chains
fit_chains <- map2stan(int_mod, data=d.trim,
chains = 4, cores=4)- Can fit with multiple chains to inspect convergence
- Yay multicore computers!
Multiple Chains
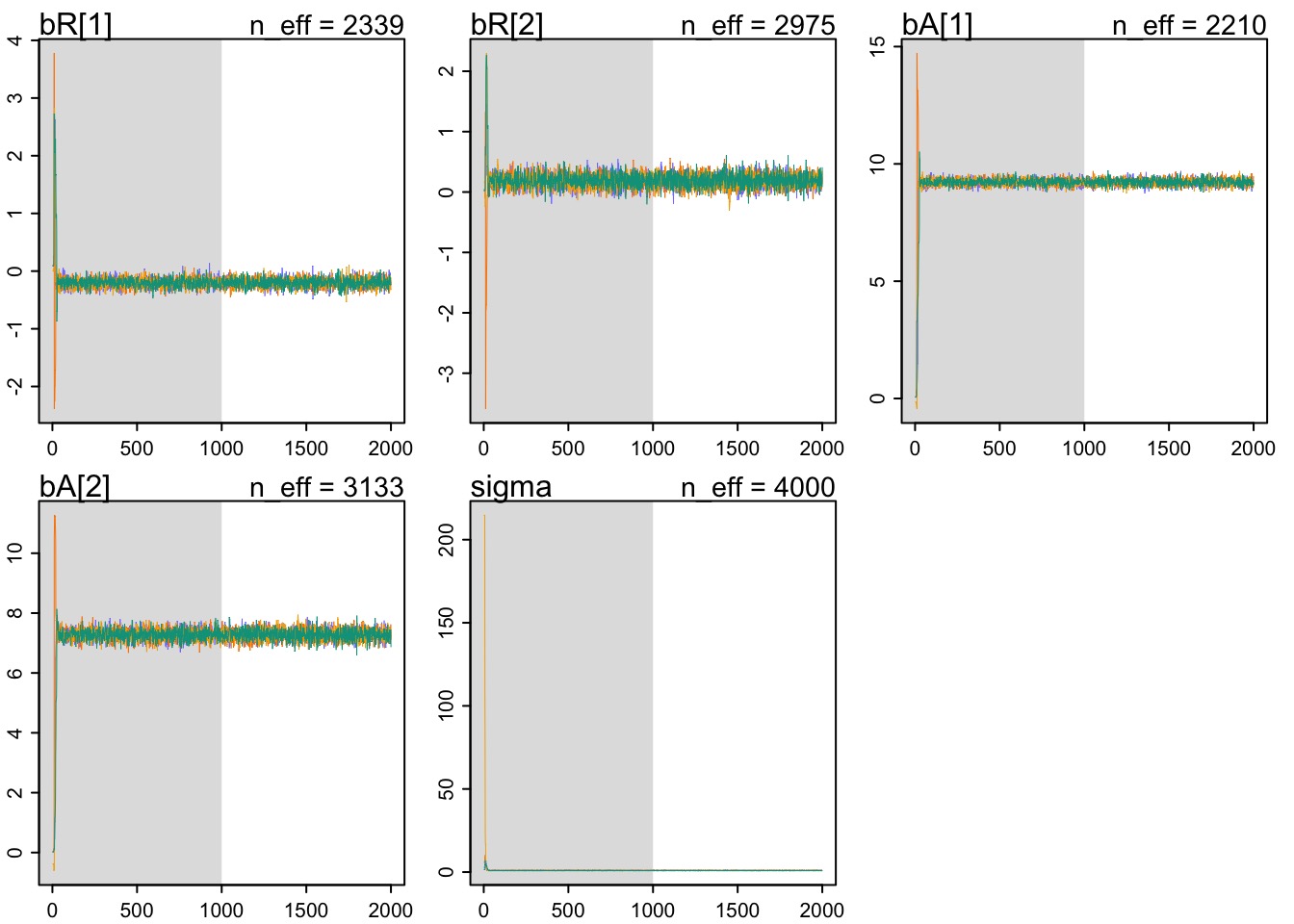
Assessing Convergence
precis(fit_chains, depth=2) Mean StdDev lower 0.89 upper 0.89 n_eff Rhat
bR[1] -0.20 0.08 -0.33 -0.08 2339 1
bR[2] 0.19 0.11 0.02 0.36 2975 1
bA[1] 9.22 0.14 9.00 9.44 2210 1
bA[2] 7.28 0.18 6.99 7.57 3133 1
sigma 0.95 0.05 0.86 1.03 4000 1n_effis effective number of samples in chain- Should be reasonably large
- Should be reasonably large
Rhatis a measure of convergence- Gelman-Rubin diagnostic
- Should be 1 - even 1.01 is suspect
- Treat as warnings - necessary but not sufficient
What do bad chains look like?
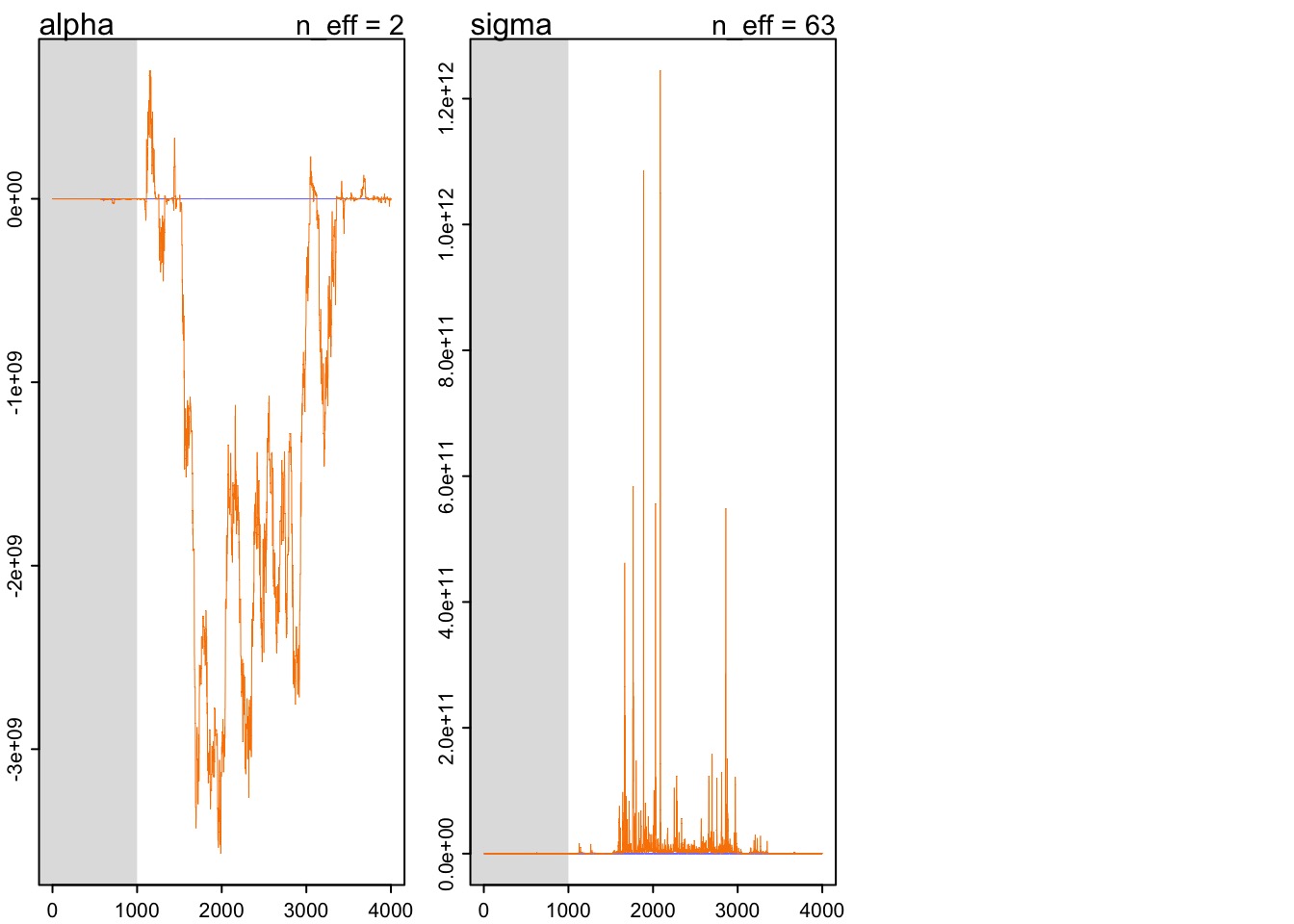
Lack of Convergence
- Might be that model has not found good values
- More likely bad model
- Too many parameters
- Redundant parameters
- Poor fit to data

- Too many parameters
General Workflow
- Fit one chain to make sure things look OK
- warmup = 1000, iter=2000 OK
- warmup = 1000, iter=2000 OK
- Fit multiple chains to ensure convergence
- Inspect
n_effandr_hat - Make sure posterior converges and is stationary
- Tune HMC and model parameters
- Inspect
- Fit one chain with large everything tuned
- Can use more chains if you have the processors
Exercise
- Refit your homework models
- Do estimates differ from MAP?
- Try uncentered model - does it perform better?