Interaction Effects


What is an interaction effect?

  • Effects of predictors no longer independent
    • Effects conditional on one another

  • May not be possible to evluate effect of single predictor in isolation

  • Generalized linear models: All predictors interact (even with themselves)
    • Effect of a variable dependent on current value of all other predictors

  • Multilevel models: slope/intercept vary by groups
    • interactions all the way down

Linear nteractions with Discrete Variables

  • Variable slope
    • Contrast to just plain olde variable intercept

  • Effect of a predictor (even intercept!) depends on what group it’s in

  • Gateway to multilevel/mixed models

How does ruggedness influence GDP?

data(rugged)
rugged$log_gdp <- log(rugged$rgdppc_2000)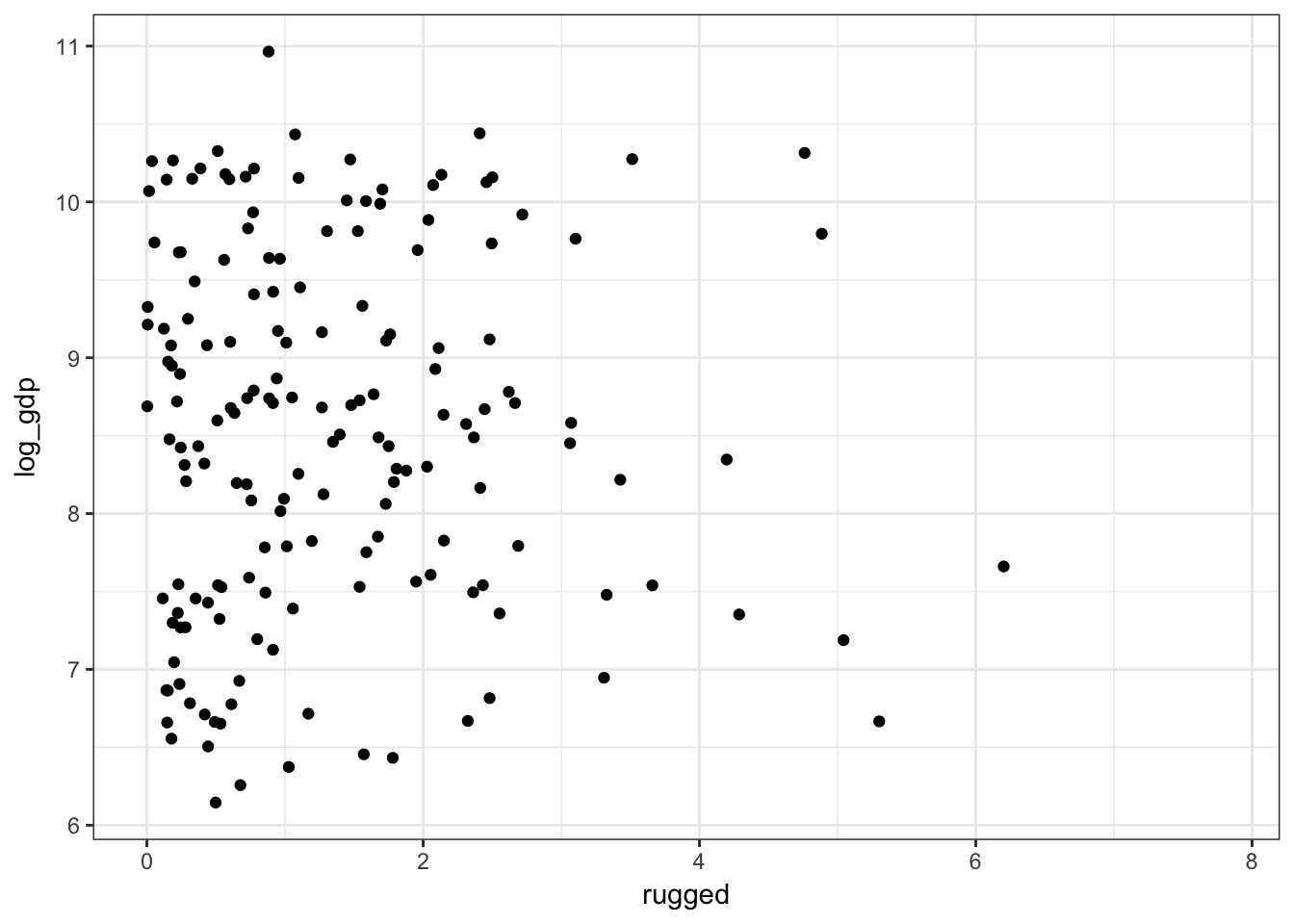

How does ruggedness influence GDP?

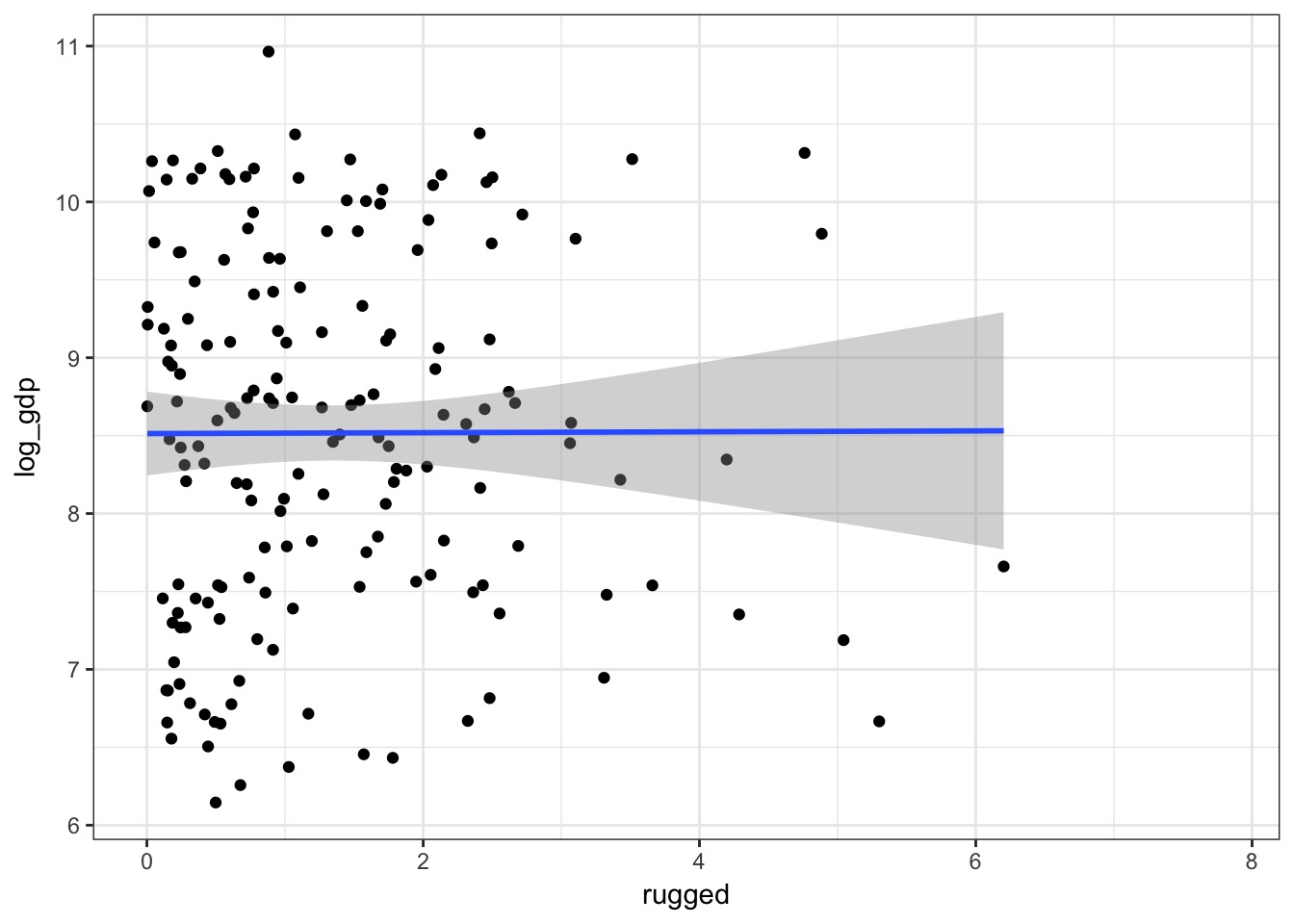
How does ruggedness influence GDP?

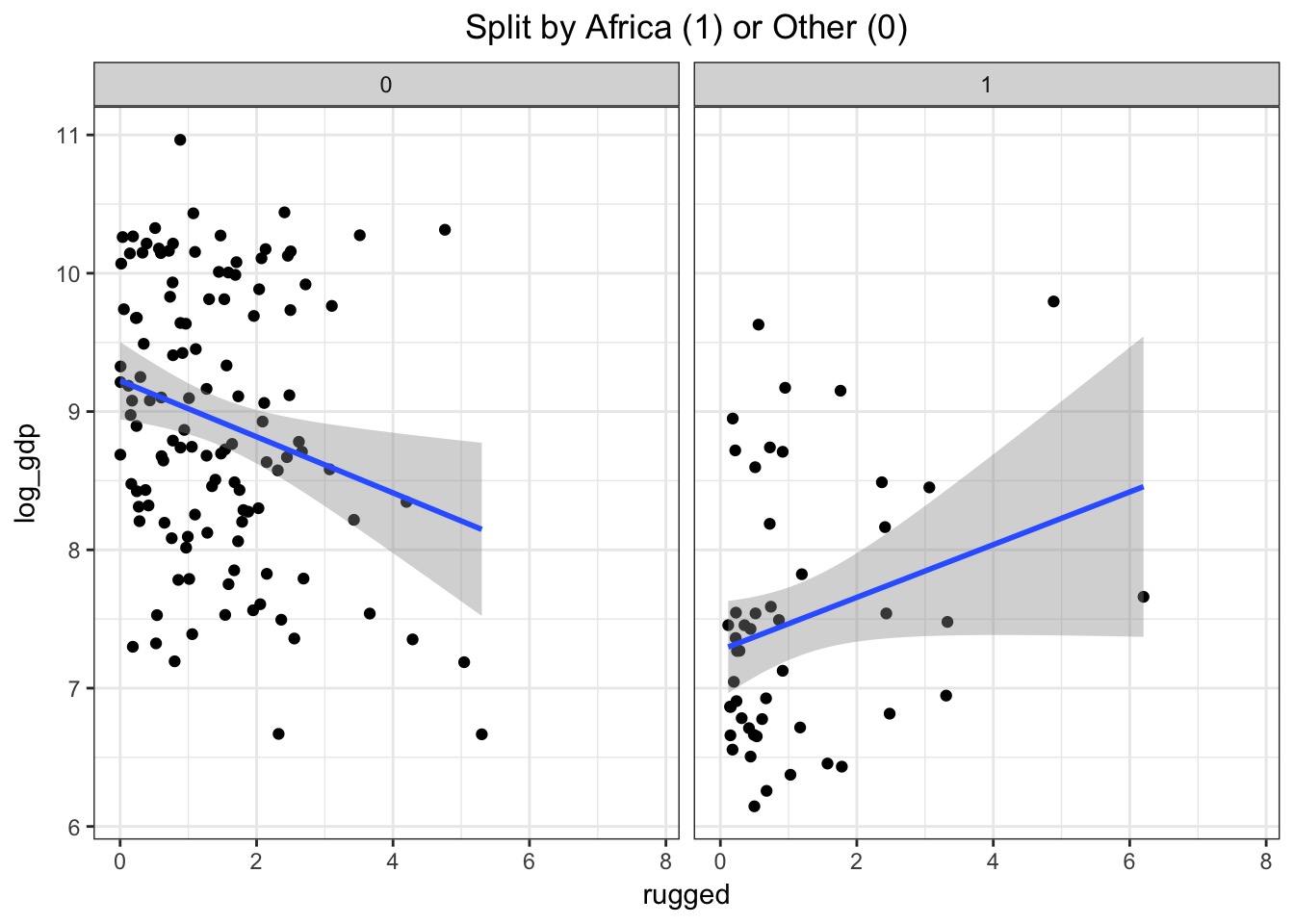
Model with No Interaction

#prep the data
d <- rugged[complete.cases(rugged$log_gdp),]

#need indices >0
d$cont_africa <- d$cont_africa +1

#The model
mod_no_int <- alist(
  #likelihood
  log_gdp ~ dnorm(mu, sigma),

  #data generating process
  mu <- bA[cont_africa] + bR*rugged,

  #priors
  bR ~ dnorm(0,1),
  bA[cont_africa] ~ dnorm(8,100),
  sigma ~ dunif(0,10))

fit_no_int <- map(mod_no_int, data=d)

What does that look like?

Variable intercept only

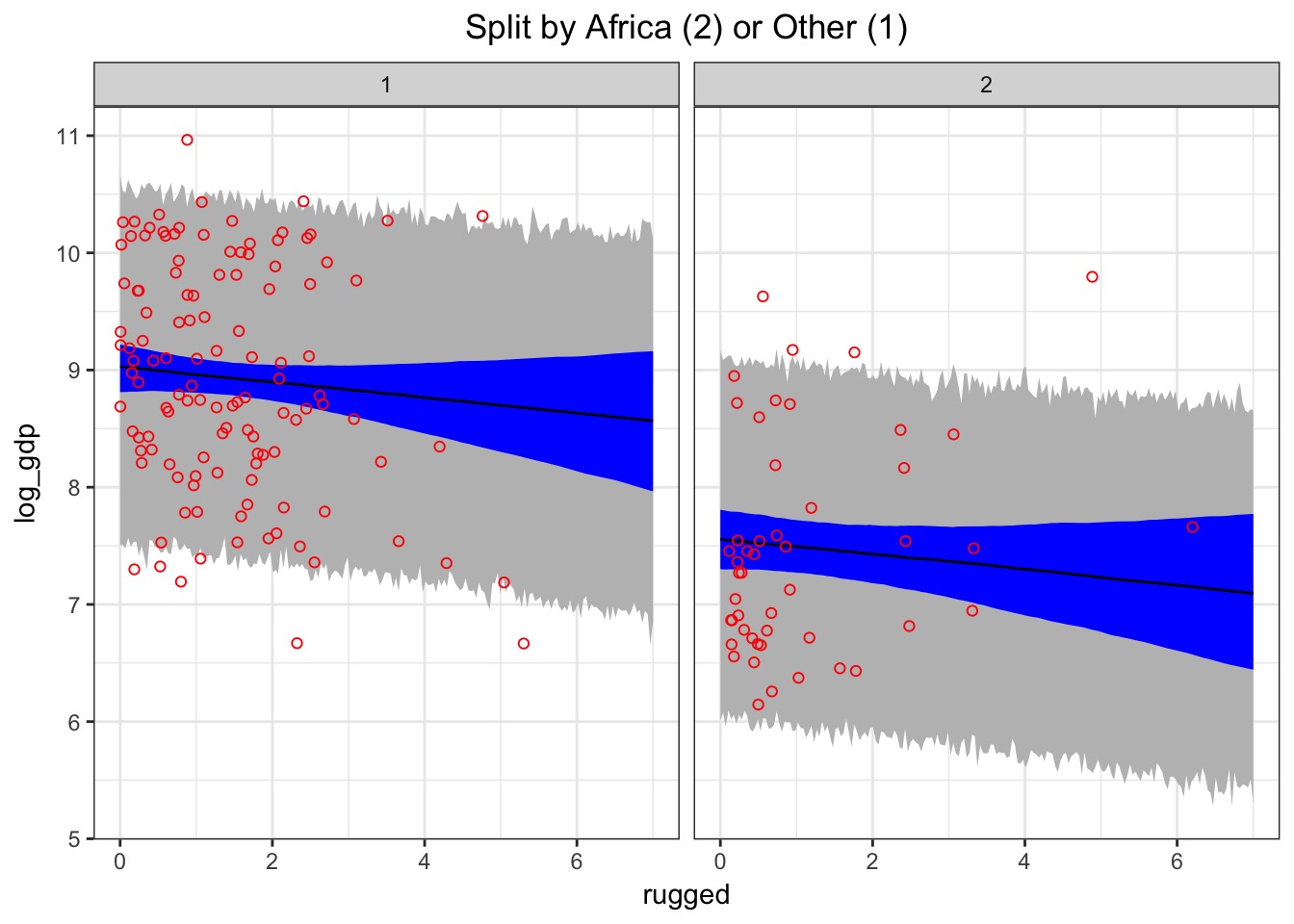
Handling Categories

No Interaction:

mu <- bA[cont_africa] + bR*rugged,

#OR

mu <- a + bA[cont_africa] + bR*rugged,

What is the difference in what these two return?

OK, so, How do we write a categorical interaction?

Interaction 1:

mu <- bA[cont_africa] + bR*rugged,

bR <- bR_0 + bR_1*cont_africa
  • Keeps form for mu but incorporates new information
  • bR_1 is difference from non-African bR

OK, so, How do we write a categorical interaction?

Interaction 2

mu <- bA[cont_africa] + bR*rugged + bR_1*cont_africa,
  • More compact
  • bR_1 has same meaning as before

OK, so, How do we write a categorical interaction?

Interaction 3

mu <- bA[cont_africa] + bR[cont_africa]*rugged,
  • Uses indexing for groups
  • No post-hoc calculation issues

The full model

int_mod <- alist(
  #likelihood
  log_gdp ~ dnorm(mu, sigma),
  
  #Data generating process
  mu <- bR[cont_africa]*rugged + bA[cont_africa],
  
  #priors - note indexing!
  bR[cont_africa] ~ dnorm(0,1),
  bA[cont_africa] ~ dnorm(8,100),
  sigma ~ dunif(0,10)
)

int_fit <- map(int_mod, data=d)

Coefficients

Note depth=2 for groups

precis(int_fit, depth=2, cor=TRUE)
       Mean StdDev  5.5% 94.5% bR___1 bR___2 bA___1 bA___2 sigma
bR[1] -0.20   0.08 -0.32 -0.08   1.00   0.00  -0.79   0.00     0
bR[2]  0.19   0.10  0.02  0.36   0.00   1.00   0.00  -0.66     0
bA[1]  9.22   0.14  9.00  9.44  -0.79   0.00   1.00   0.00     0
bA[2]  7.28   0.18  6.99  7.56   0.00  -0.66   0.00   1.00     0
sigma  0.93   0.05  0.85  1.01   0.00   0.00   0.00   0.00     1
Note that bR changes in sign between groups!

Inspection

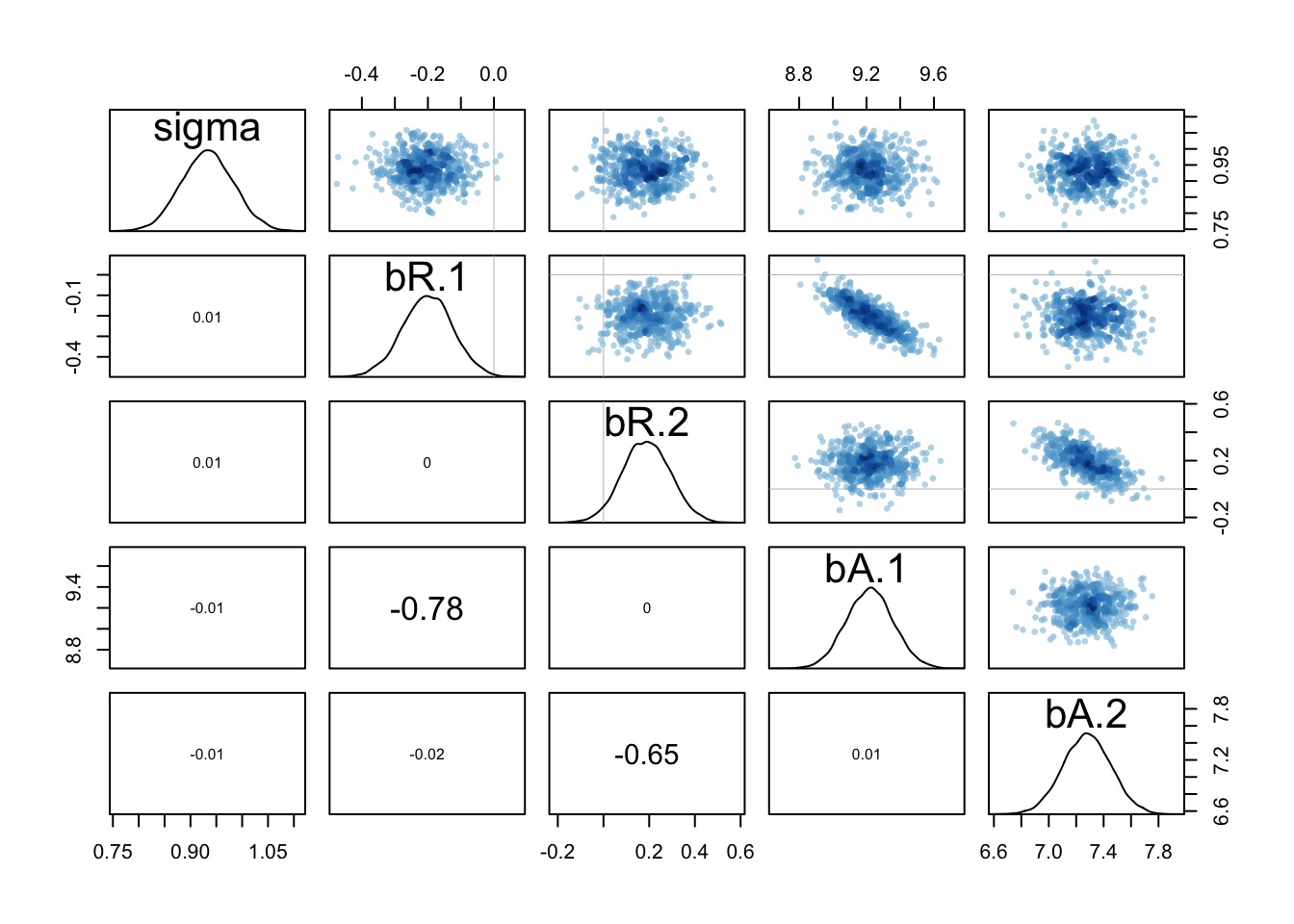
A posthoc: Are slopes really different?

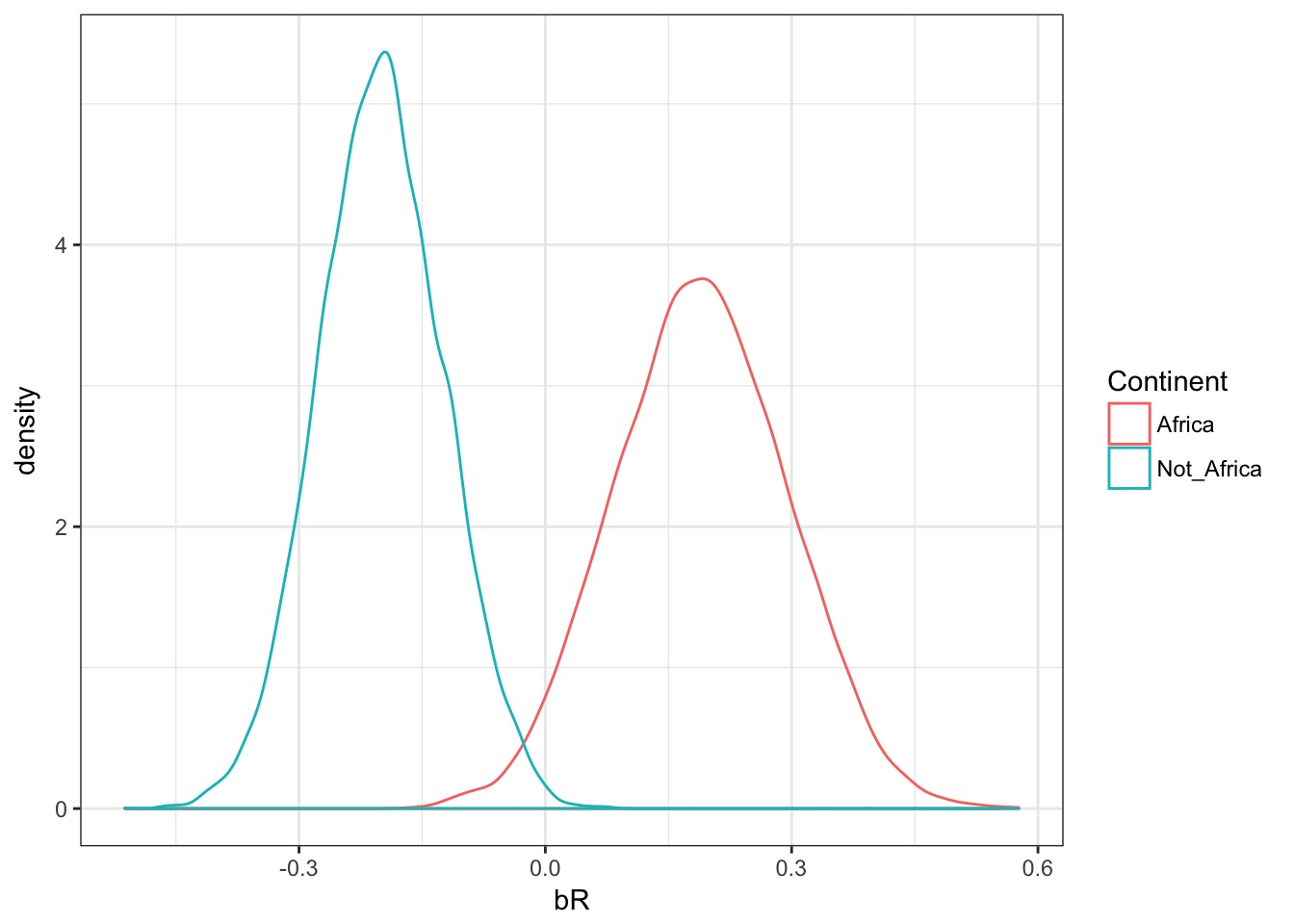
Calculate the difference

samps <- extract.samples(int_fit)

names(samps)
[1] "sigma" "bR"    "bA"   
head(samps$bR)
            [,1]       [,2]
[1,] -0.15179570 0.27818267
[2,] -0.17523714 0.09972111
[3,] -0.15245867 0.34652585
[4,] -0.09268935 0.11231884
[5,] -0.14039837 0.25779016
[6,] -0.19623546 0.21929095
#Not Africa v. Africa
diff_br <- samps$bR[,1] - samps$bR[,2]

Were they different?

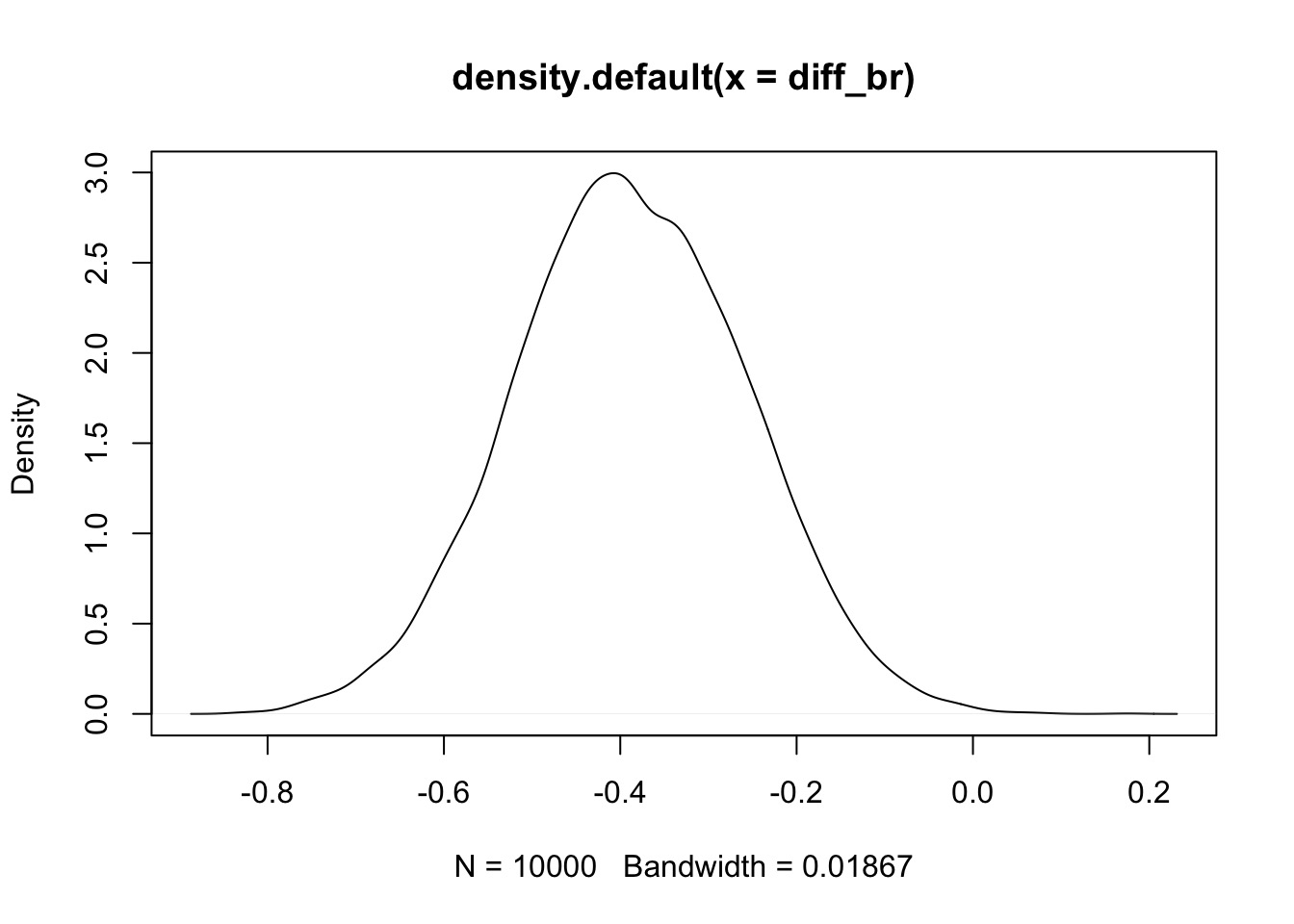
99.9% were < 0
They are quite likely different

Interpretation

What can you say so far?

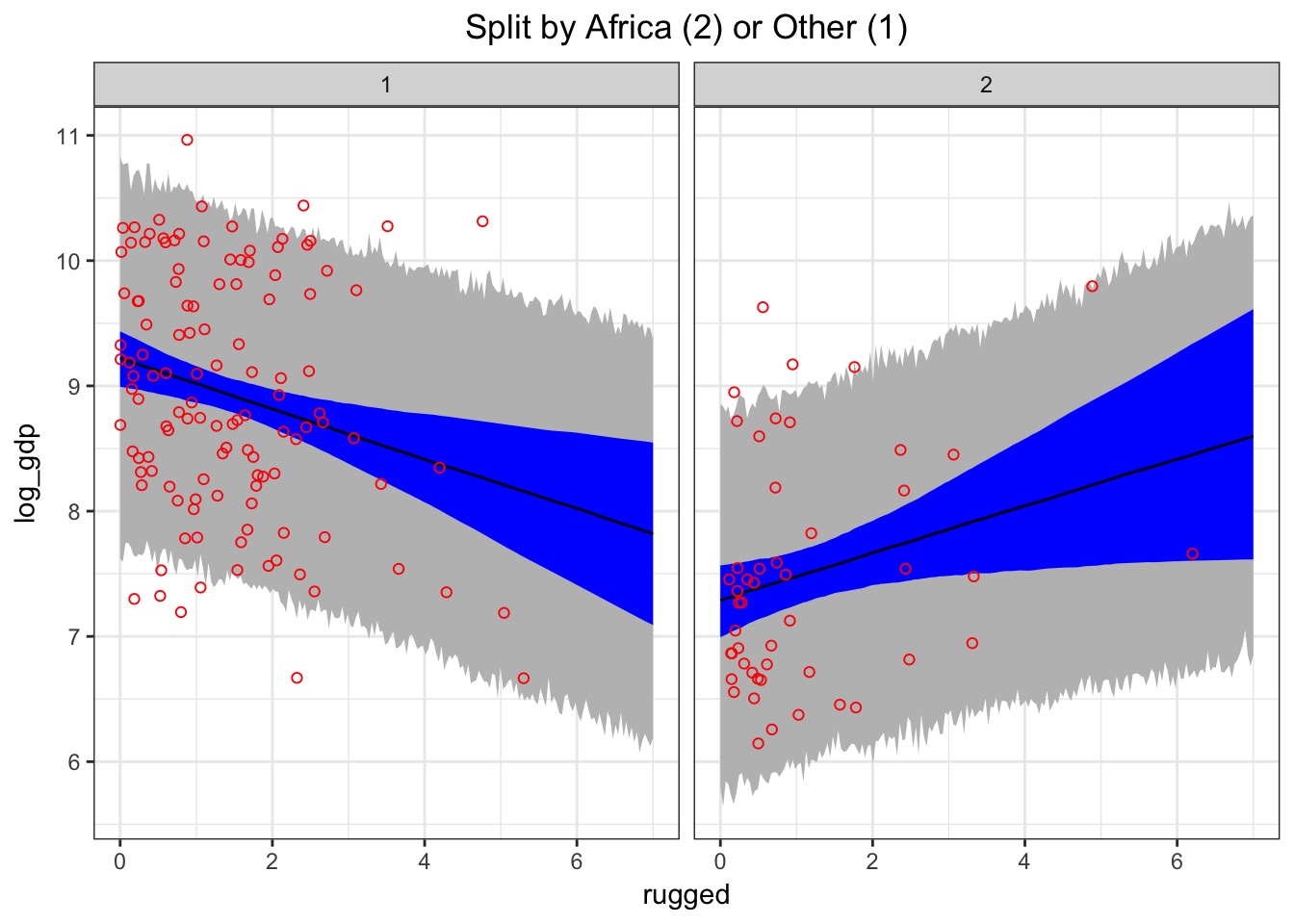
Continuous Interactions

  • Effects of predictors no longer independent
    • Effects conditional on one another

  • May not be possible to evluate effect of single predictor in isolation

  • Require counterfactual plots to assess meaning

Tulips!

data(tulips)
head(tulips)
  bed water shade blooms
1   a     1     1   0.00
2   a     1     2   0.00
3   a     1     3 111.04
4   a     2     1 183.47
5   a     2     2  59.16
6   a     2     3  76.75

Continuous Interactions are Simple to Code

tulip_mod <- alist(
  #likelihood
  blooms ~ dnorm(mu, sigma),
  
  #Data generating process
  mu <- a + bW*water + bS*shade + bWS*water*shade,
  
  #priors
  a ~ dnorm(130,100),
  bW ~ dnorm(0,100),
  bS ~ dnorm(0,100),
  bWS ~ dnorm(0,100),
  sigma ~ dunif(0,100)
)

Common fitting errors!

fit_tulip <- map(tulip_mod, data=tulips)
Error in map(tulip_mod, data = tulips): non-finite finite-difference value [5]
Start values for parameters may be too far from MAP.
Try better priors or use explicit start values.
If you sampled random start values, just trying again may work.
Start values used in this attempt:
a = 150.331309039261
bW = 187.446212728008
bS = -41.3825724654428
bWS = 80.3598233487261
sigma = 60.5601385002956

Fixes

  1. Try a different algorithm
    • Nelder-Mead often works, but slower
    • SANN also works, but sloooow

  2. Transform values
    • Center
    • Scale
  3. Supply start values

  4. Change priors

  5. Change algorithmic parameters

These both work

fit_tulip_1 <- map(tulip_mod, 
                   data=tulips,
                   method="Nelder-Mead")

or

tulip_cent <- tulips %>% mutate(shade = shade-mean(shade),
                                          water = water-mean(water))
fit_tulip_2 <- map(tulip_mod, 
                   data=tulip_cent)

How does the meaning change with centering?

      fit_tulip_1 fit_tulip_2
a      -49.50      128.98    
bW     136.79       74.97    
bS      20.49      -41.12    
bWS    -33.70      -51.95    
sigma   47.37       45.25    
nobs       27          27
And, what do these coefficients say?

Counterfactal Plots are Necessary

tulip_pred_df <- crossing(shade = -1:1, water = -1:1)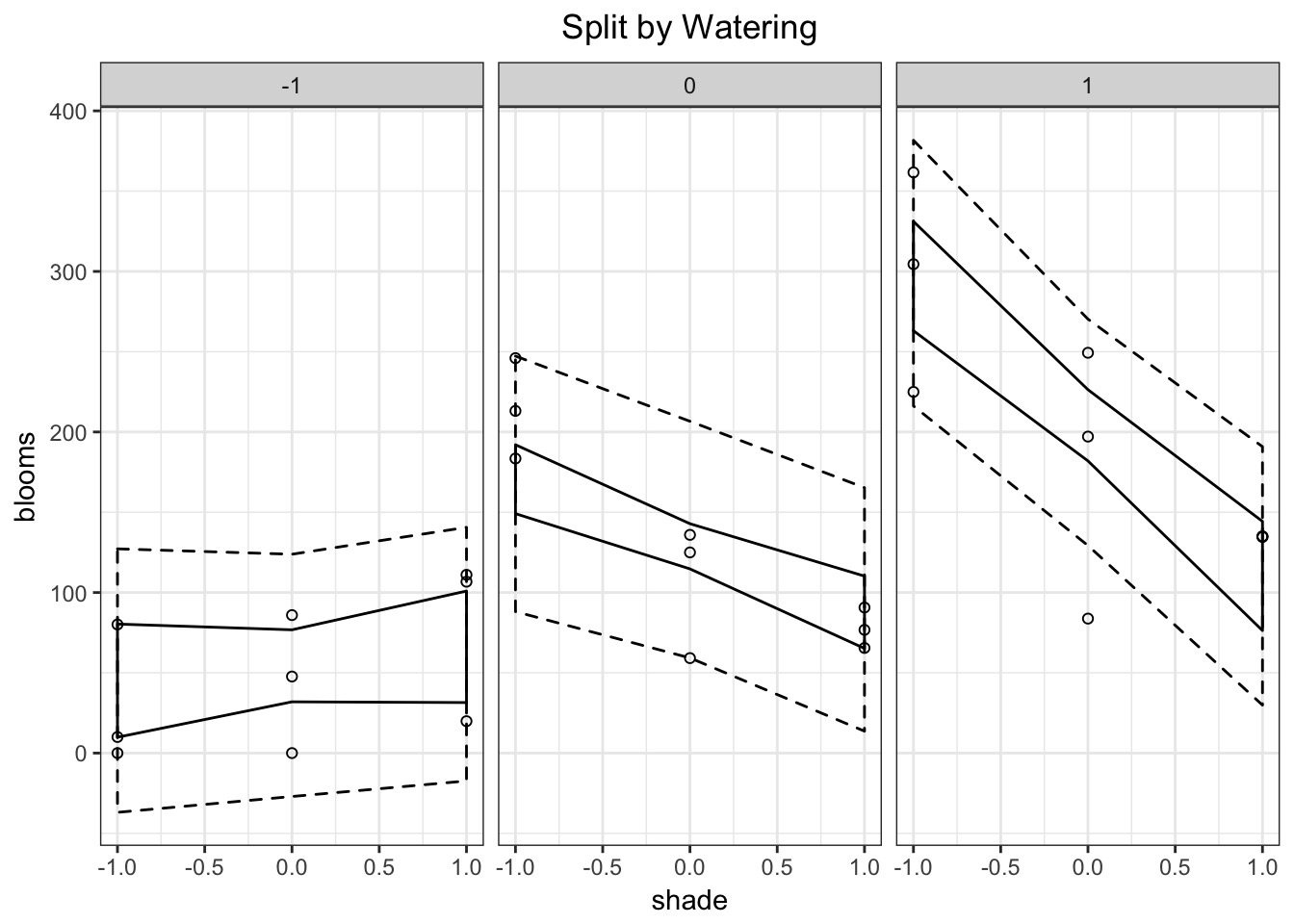

Exercise

  1. Take the excellent milk models you have!

  2. Now, make models where
    1. Effects vary by clade AND/OR
    2. Different predictors interact

  3. Evaluate with WAIC

  4. Plot implications to understand
    • Single model or ensemble

  5. Go green if you have something cool to throw up