Sampling Your Posterior

The data

So, we’ve flipped the globe 6 times, and drawn W,L,W,W,W,L,W,L,W

water <- 6

Grid Sampling

In a data frame:
1. Use seq to come up with a set of possible probability values

2. Add a column of priors. Make it flat, so they’re all 1, or get fancy.

3. Calculate your likelihoods for each probability with size=9 and W=6

4. Calculate your prior * likelihood

5. Calculate your posterior, as the previous value divided by the sum of all prior*likelihoods

And we’ve made a grid sample

library(dplyr)

# our hypotheses and prior = 1/nrow
grid <- data.frame(prob = seq(0,1,.01), 
                   prior=1/101) |>
  
  #calculate likelihood
  mutate(likelihood = 
           dbinom(water, size = 9, prob = prob)) |>
  
  # multiply by prior
  mutate(posterior = likelihood*prior) |>
  
  # divide by marginal (normalize)
  mutate(posterior = posterior/sum(posterior))

Note - if rounding error is a problem

# our hypotheses
log_grid <- data.frame(prob = seq(0,1,.01), 
                   prior=1/101) |>
  
  #calculate log likelihood
  mutate(likelihood = 
           dbinom(water, size = 9, prob = prob, log = TRUE)) |>
  
  # multiply by prior
  mutate(posterior = likelihood + prior) |>
  
  # exponentiate and divide by marginal (normalize)
  mutate(posterior = exp(posterior),
         posterior = posterior/sum(posterior))




How do we query our posterior?

Our posterior

head(grid)
  prob      prior   likelihood    posterior
1 0.00 0.00990099 0.000000e+00 0.000000e+00
2 0.01 0.00990099 8.150512e-11 8.150511e-12
3 0.02 0.00990099 5.059848e-09 5.059848e-10
4 0.03 0.00990099 5.588844e-08 5.588844e-09
5 0.04 0.00990099 3.044058e-07 3.044058e-08
6 0.05 0.00990099 1.125305e-06 1.125305e-07

Our posterior at it’s peak

grid |> 
  arrange(desc(posterior)) |> 
  head()
  prob      prior likelihood  posterior
1 0.67 0.00990099  0.2730674 0.02730674
2 0.66 0.00990099  0.2728850 0.02728850
3 0.68 0.00990099  0.2721339 0.02721339
4 0.65 0.00990099  0.2716211 0.02716211
5 0.69 0.00990099  0.2700592 0.02700591
6 0.64 0.00990099  0.2693188 0.02693188

What does it look like?

Code

library(ggplot2)
theme_set(theme_classic(base_size = 14))

ggplot(grid, aes(x = prob, y = posterior)) + geom_line()

How do we query our posterior?

  1. We could look at all values of the posterior and calcuate the density

  2. We could look at the highest posterior or weighted average

  3. We could integrate over a selected range and…

AH! Intergrals? No! Samples? Yes!

  • Posteriors summarize the frequency of certain values

  • We can leverage that and use our grid sample to generate an empirical distribution

  • This lets us develop an intuitive notion of the posterior, and manipulate it easily

Sampling from your Posterior

samp <- tibble(
  draw = 1:1e4,
  
  samp = sample(grid$prob, # parameters
               
               size = 1e4,  #how many draws
               
               replace=TRUE, # sample with replacement
               
               prob = grid$posterior) # probability of each parameter
)

Sampling from your Posterior

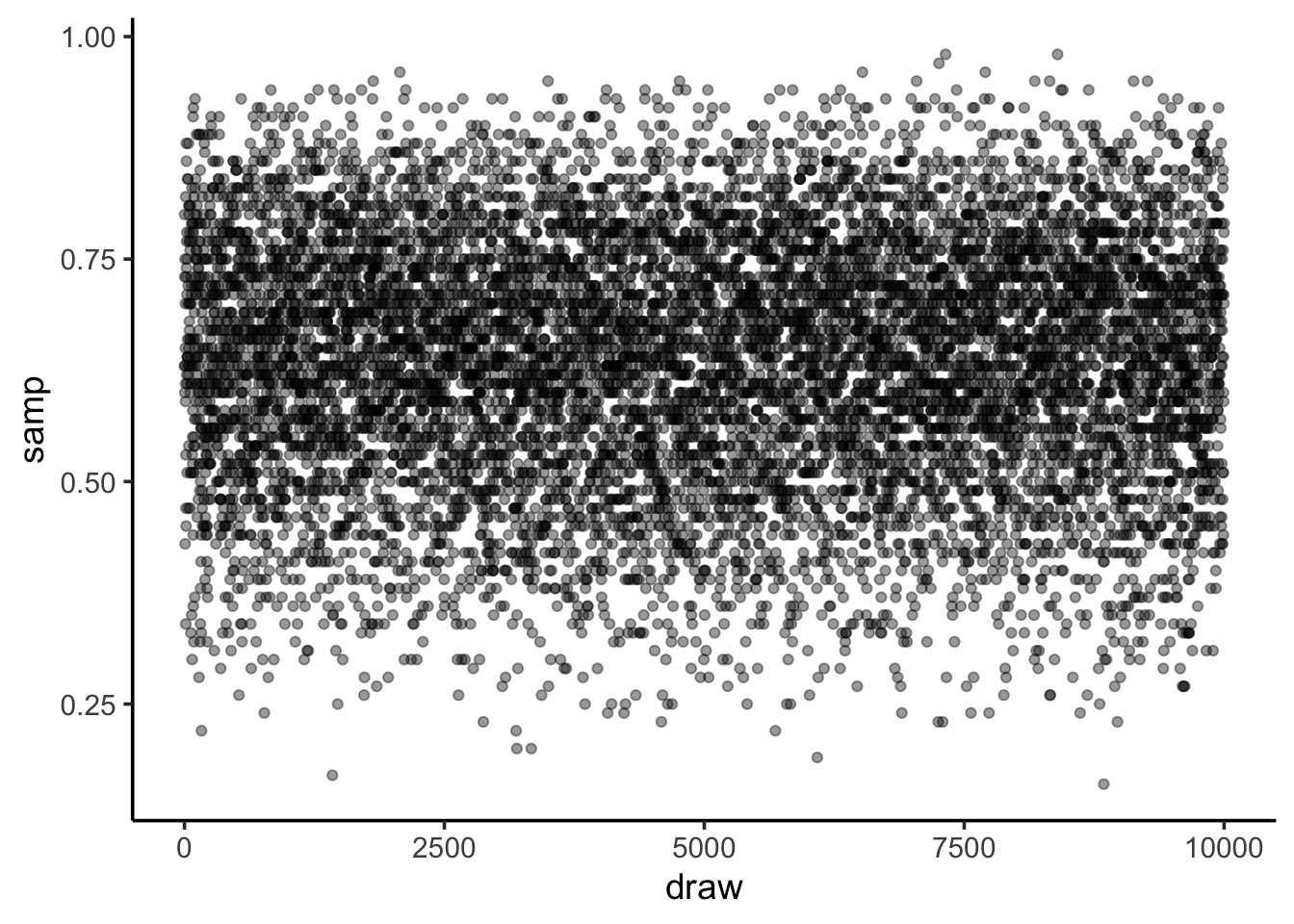
Code

ggplot(samp, aes(x = draw, y = samp)) +
  geom_point(alpha = .4)

Sampling from your Posterior: MCMC style

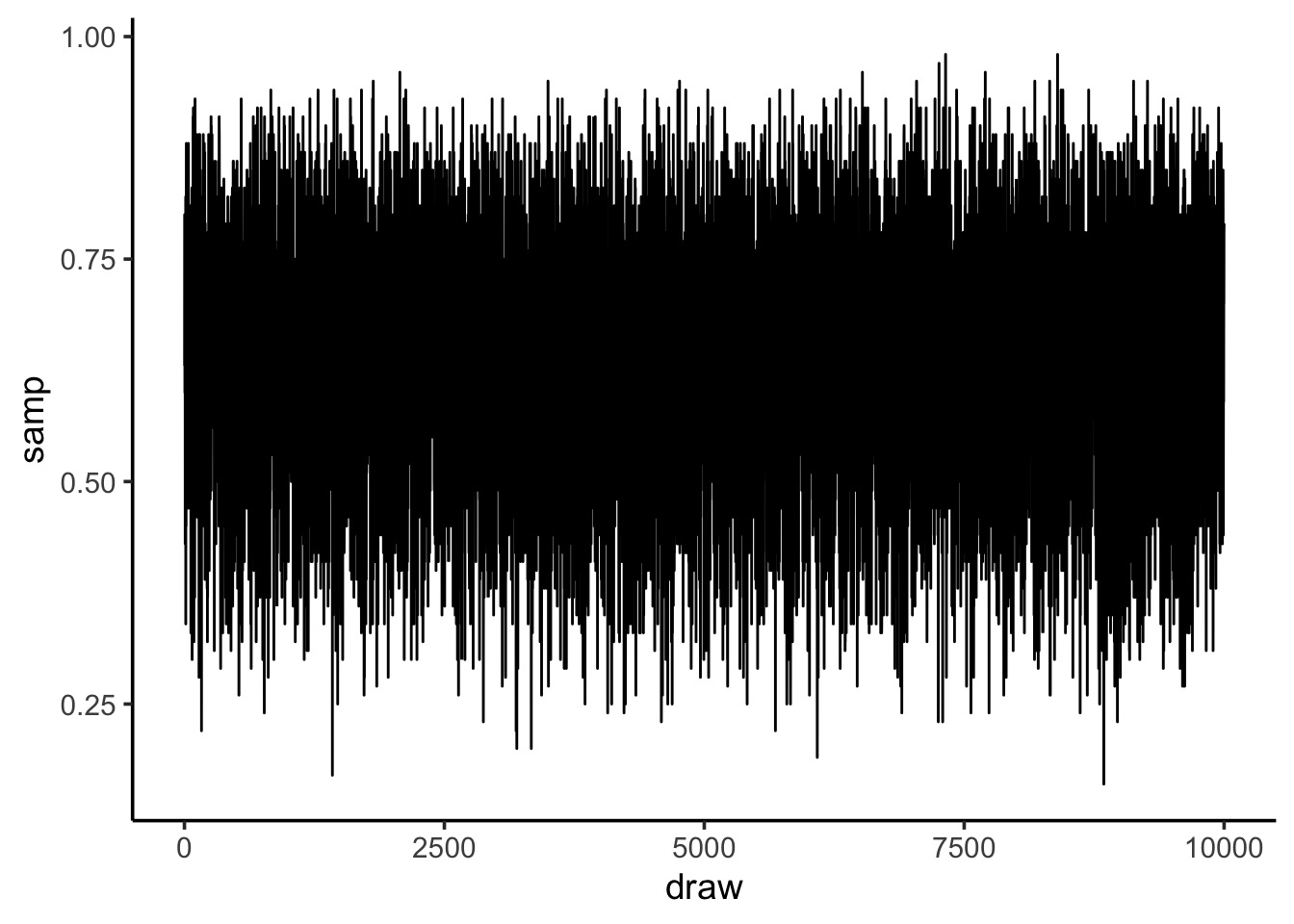
Code

ggplot(samp, aes(x = draw, y = samp)) +
  geom_line(alpha = 1)

What can we do with this: histogram

Code

ggplot(samp, aes(x = samp)) +
  geom_histogram(bins = 40)+ 
  labs(subtitle = "40 bins")

Histograms can show weakness of grid

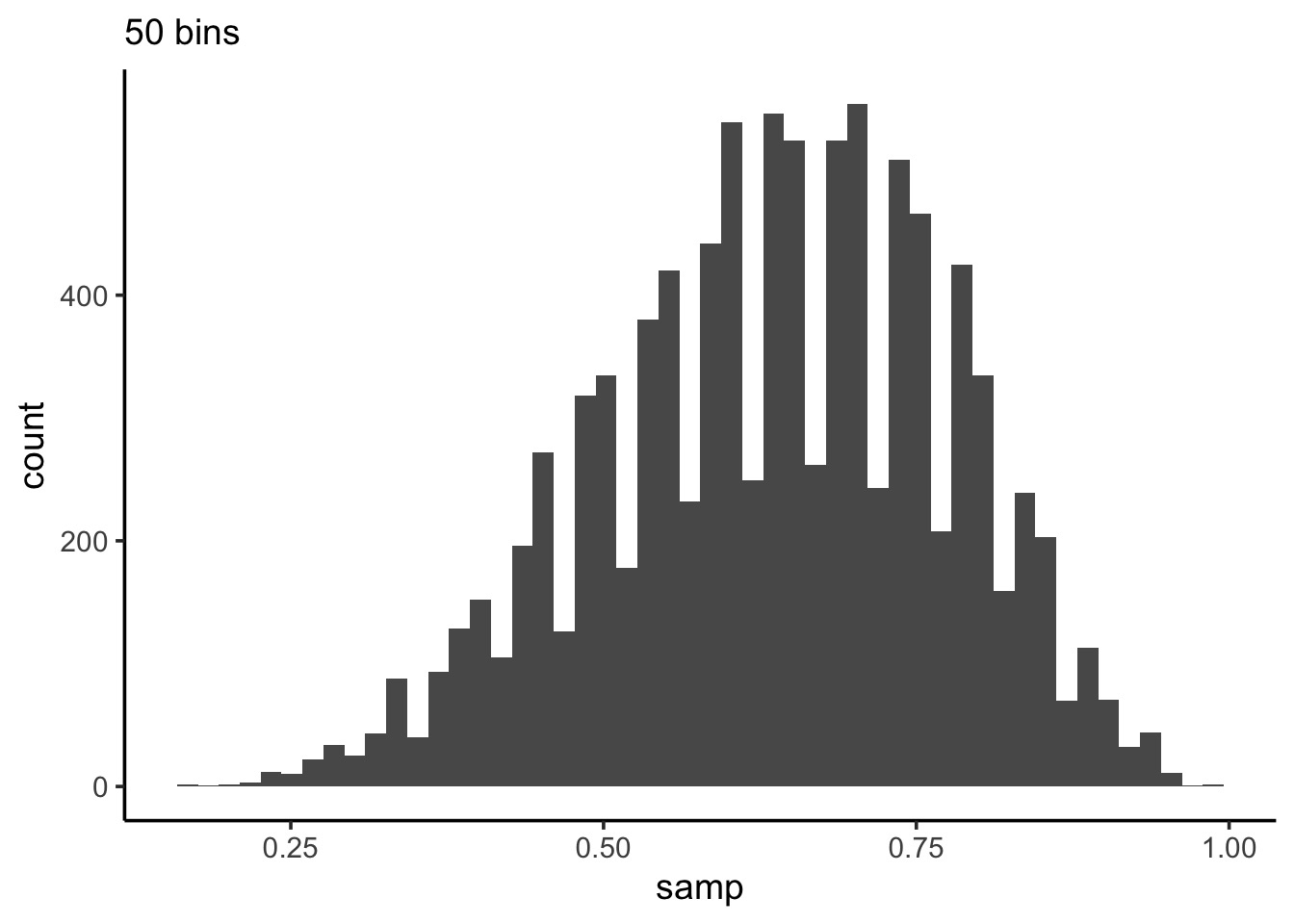
Code

ggplot(samp, aes(x = samp)) +
  geom_histogram(bins = 50) + 
  labs(subtitle = "50 bins")

What can we do with this: density

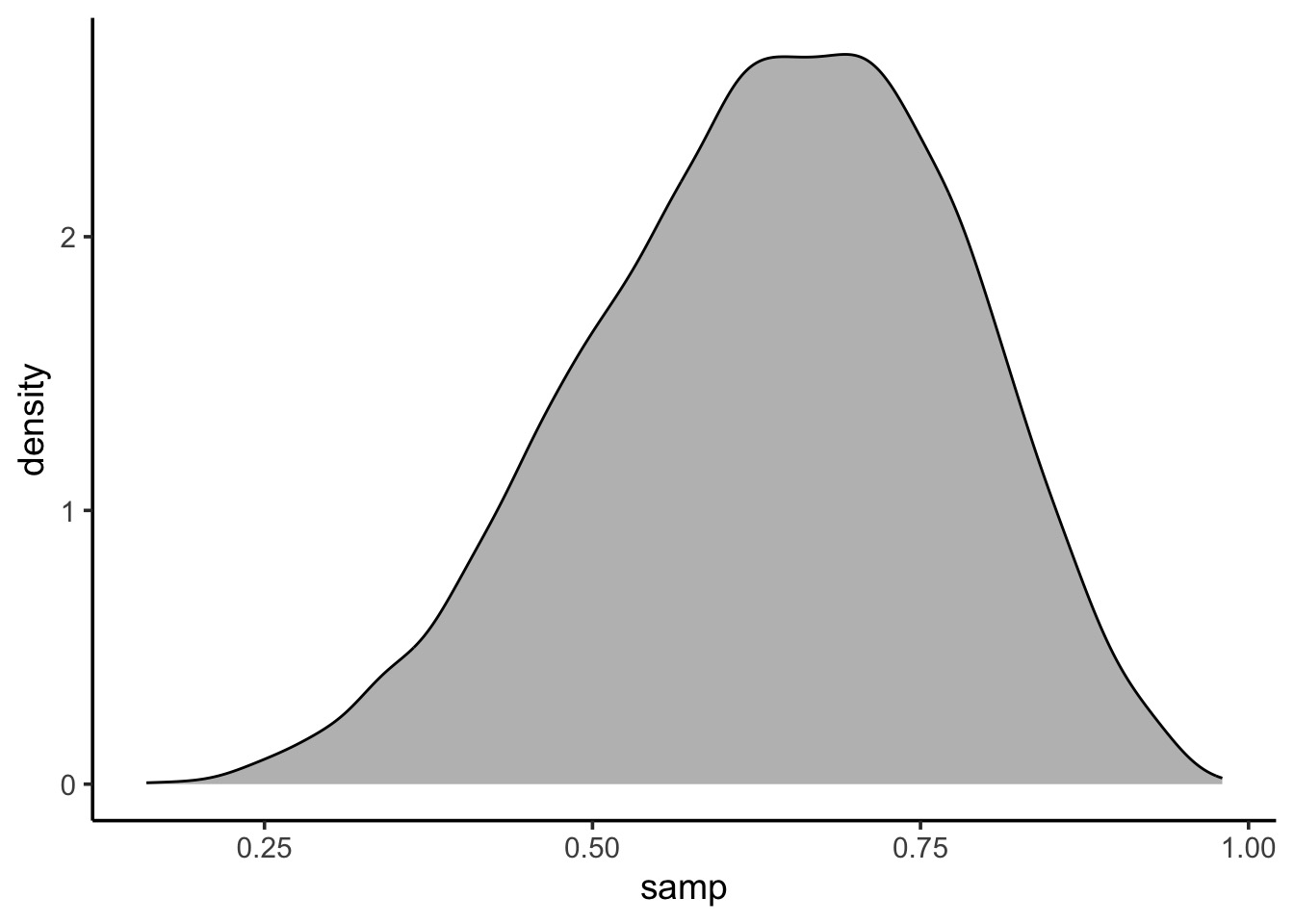
Code

ggplot(samp, aes(x = samp)) +
  geom_density(fill = "grey")




Summarizing a Parameter with a Sample

Summarizing a sample of a posterior: Questions we can ask

How much of the posterior is less than a certain value?

How much of the posterior is greater than a certain value?

What value of the posterior has the highest density?

What is the range of the values of some percent of the posterior? e.g., 90%

Looking at mass < a key value

  • Let’s say we wanted the % of the posterior < 0.4

sum(samp$samp < 0.4) / nrow(samp)
[1] 0.0504

So, 5.04% of the posterior

Plotting an Interval

Code:

It’s a filter thang!

ggplot() +
  
  #grid posterior
  geom_line(data = grid,
               aes(x = prob, y = posterior)) +
  
  #the interval
  geom_ribbon(data = grid |> filter(prob < 0.4), #interval
              ymin = 0, aes(x = prob, ymax = posterior), #top and bottom
              fill = "black")

Try a few

  • What % is < 0.6

  • What % is > 0.6

  • What % is between 0.2 and 0.6

How do we describe a parameter

  • Typically we want to know a parameter estimate and information about uncertainty

  • Uncertainty can be summarized via the distribution of a large sample
    • We can look at credible (compatability) intervals based on mass of sample

  • We have a few point estimates we can also draw from a sample
    • Mean, median, mode

Summarizing Uncertainty: 50th Percentile Interval

We often look at the 95% credible interval

quantile(samp$samp, c(0.025, 0.975))
 2.5% 97.5% 
 0.35  0.88

But this is arbitrary (thanks, Fisher), and unstable.
Lower intervals are more stable - e.g., the 50% credible Interval

quantile(samp$samp, c(0.25, 0.75))
 25%  75% 
0.54 0.74

Summarizing Uncertainty: Percentiles

We can calculate quantiles using the cummulative density of the posterior

grid <- grid |>
  mutate(quantile = cumsum(posterior)/sum(posterior))

Summarizing Uncertainty: 50th Percentile Interval

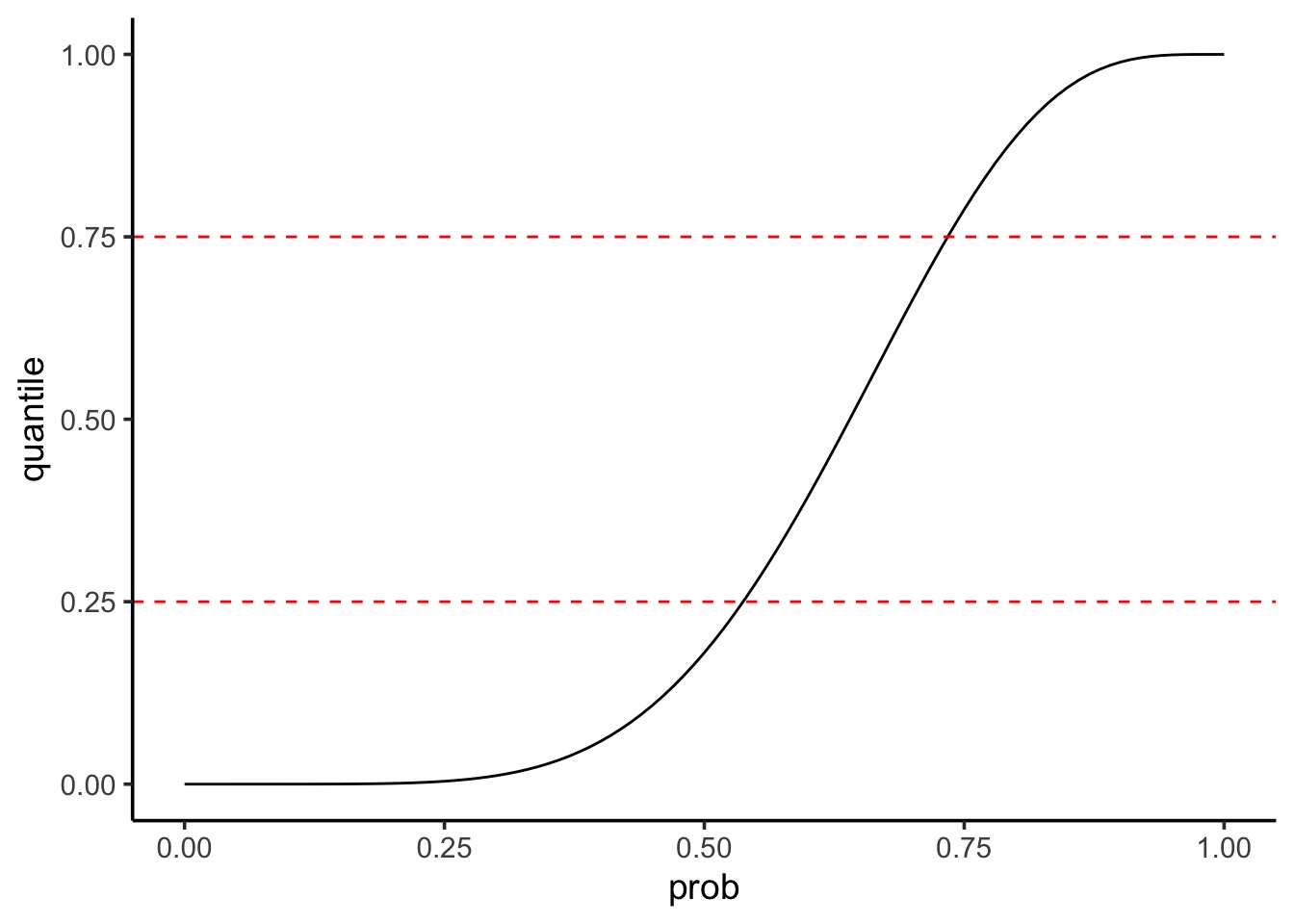
Code

ggplot(grid, aes(x = prob, y = quantile)) +
  geom_line() +
  geom_hline(yintercept = 0.25, color = "red", lty = 2) +
  geom_hline(yintercept = 0.75, color = "red", lty = 2)

Summarizing Uncertainty: 50th Percentile Interval

Visualize as before

Summarizing Uncertainty: 50th Percentile Interval Code

Visualize as before

ggplot() +
  
  #grid posterior
  geom_line(data = grid,
               aes(x = prob, y = posterior)) +
  
  #the interval
  geom_ribbon(data = grid |> filter(quantile > 0.25 & quantile < 0.75),
              ymin = 0, aes(x = prob, ymax = posterior),
              fill = "black")

Note that this is not the Highest Posterior Density Interval

PI v. HPDI

  • Percentile Intervals get interval around median that covers X% of the distribution

  • Highest Posteriod Density Interval gets interval with highest density containing 50% of mass of distribution
library(rethinking)
PI(samp$samp, 0.5)
 25%  75% 
0.54 0.74 
HPDI(samp$samp, 0.5)
|0.5 0.5| 
0.54 0.73

PI v. HPDI for a Skewed Distribution

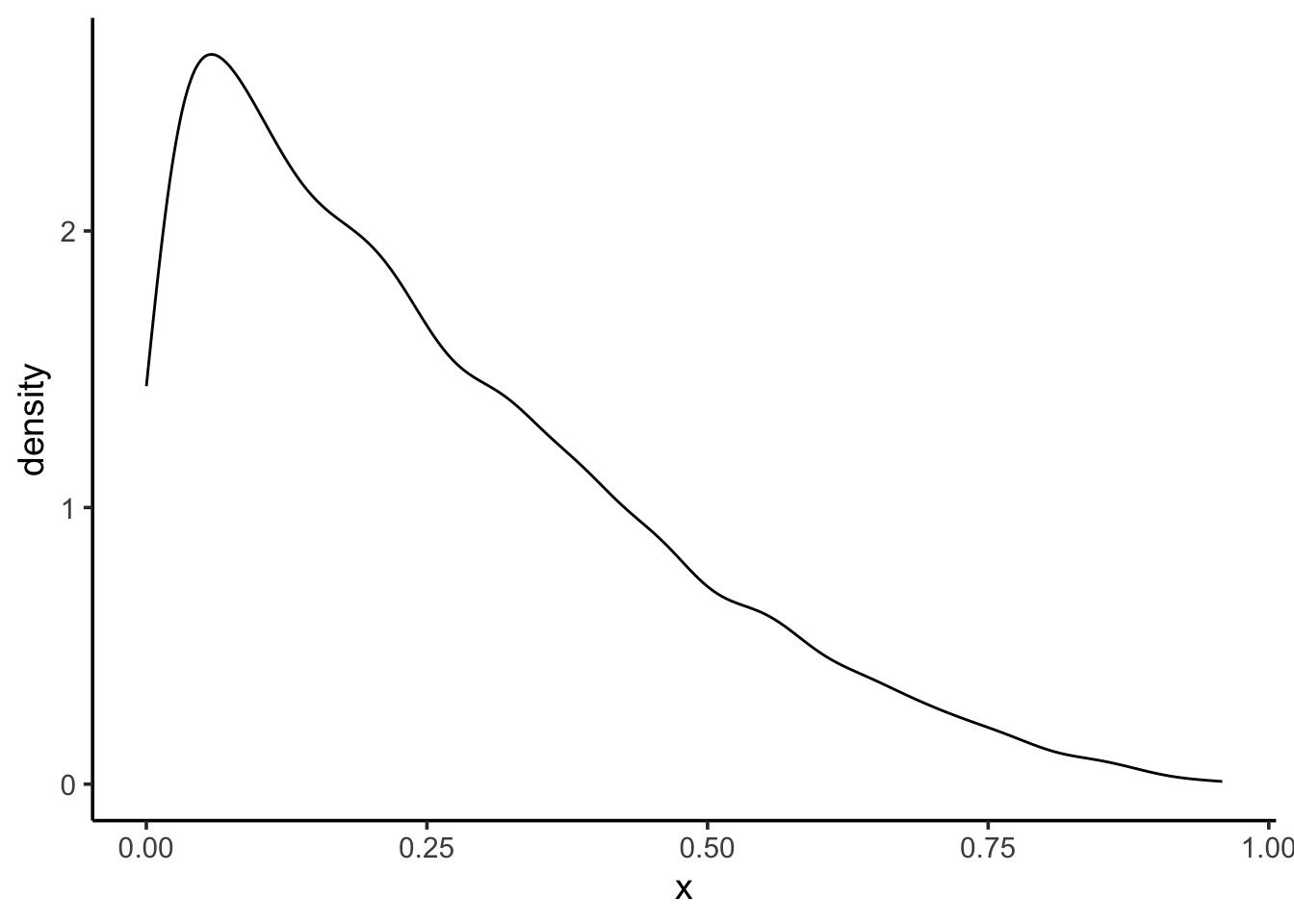
Code

ggplot(data = tibble(x = rbeta(1e4, 1,3)), aes(x=x)) +
  geom_density()

PI v. HPDI for a Skewed Distribution

samp_bad <- rbeta(1e4, 1,3)

PI(samp_bad, 0.5)
       25%        75% 
0.09251207 0.37267543 
HPDI(samp_bad, 0.5)
        |0.5         0.5| 
9.248308e-05 2.082650e-01

PI v. HPDI

Code for HPDI and PI

# to get distributional properties
dens <- density(samp_bad)
hpdi_50 <- HPDI(samp_bad, 0.5)

#properties
interval_dat <- tibble(
  prob = dens$x, # parameters
  dens = dens$y/sum(dens$y), #standardized density
  quant = cumsum(dens), #quantiles based on std dens
  
  # use the quantiles for the PI
  pi_50 = ifelse(quant >= 0.25 & quant <= 0.75,
                 dens,
                 NA),
  
  # use the values from the HPDI for filtering
  hpdi_50 = ifelse(prob >= hpdi_50[1] & prob <= hpdi_50[2],
                 dens,
                 NA)
) |>
  tidyr::pivot_longer(cols = c(pi_50, hpdi_50))

## Plot!
ggplot(interval_dat, 
       aes(x = prob, y = dens)) +
  geom_line() +
  geom_ribbon(ymin = 0, aes(ymax = value), 
              fill = "darkgrey") +
  facet_wrap(vars(name))

So which interval to use?

  • Usually, they are quite similar

  • PI communicates distirbution shape for parameter

  • HPDI matches more with the mass of the parameter that is consistent with the data

  • BUT - computationally intensive and sensitive to # of posterior draws

  • If the two are very different, the problem is not which interval type to use
    • It’s in your model/data! Buyer beware! SHOW YOUR POSTERIOR!

Which Point Estimate: Mean, Median, Mode?

mean(samp$samp)
[1] 0.636778
median(samp$samp)
[1] 0.65
#mode using max value from posterior
samp$samp[which.max(grid$posterior)]
[1] 0.71

Applying a Loss Function!

  • Well, let’s think about the cost of getting it wrong!

  • Assume a point estimate of d

  • The cost of being wrong if using d is:
    \(\sum{posterior * \left |(d-p)\right |}\)

  • Could have also squared or done other things depending on cost of being wrong

  • Can apply this to chosing \(\alpha\) and \(\beta\) in frequentist stats!

Linear Loss Function Says Median (it’s close)!

# what is the cost of a given value being wrong
# for any parameter - linear addition
loss_fun <- function(d) {
  
  dist_from_each_hypothesis <- abs(d - grid$prob)

  scaled_distance_by_posterior_prob <- 
    grid$posterior * dist_from_each_hypothesis
  
  cost_if_parameter_is_wrong <- sum(scaled_distance_by_posterior_prob)
  
}

Linear Loss Function Says Median (it’s close)!

# iterate over all parameters
loss <- sapply(grid$prob, loss_fun)

# and the point estimate with the lowest cost is...
grid$prob[which.min(loss)]
[1] 0.64
median(samp$samp)
[1] 0.65
If we had summed the squares, it would be mean! Or you can apply other functions depending on severity of cost

Choosing a loss function

  • Usually the mean and median will agree

  • If the cost of being wrong is higher, go with the mean

  • If this is a big problem, or big discrepancy, problem might be deeper
    • Examine your posterior! All of it!




Using your samples for model checking

Model Checking - Why?

  • We’re in Simulation land

  • A lot can go wrong do to small errors in our model

  • A lot can go wrong because of big errors in our model

  • Maybe our software failed (i.e., convergence)

  • Maybe our sampling design cannot produce valid estimates

How do you check models?

  • Did you reproduce your observed summarized data?

  • Did you reproduce patterns in your raw data?

Simulating from your Posterior

  • Make random draws using your sampled parameters
# Random numbers are the core of simulation!
w <- rbinom(1e4, size=9, prob = samp$samp)
janitor::tabyl(w)
 w    n percent
 0   10  0.0010
 1  124  0.0124
 2  336  0.0336
 3  780  0.0780
 4 1282  0.1282
 5 1754  0.1754
 6 1972  0.1972
 7 1858  0.1858
 8 1311  0.1311
 9  573  0.0573

Simulating from your Posterior Sample

simplehist(w)

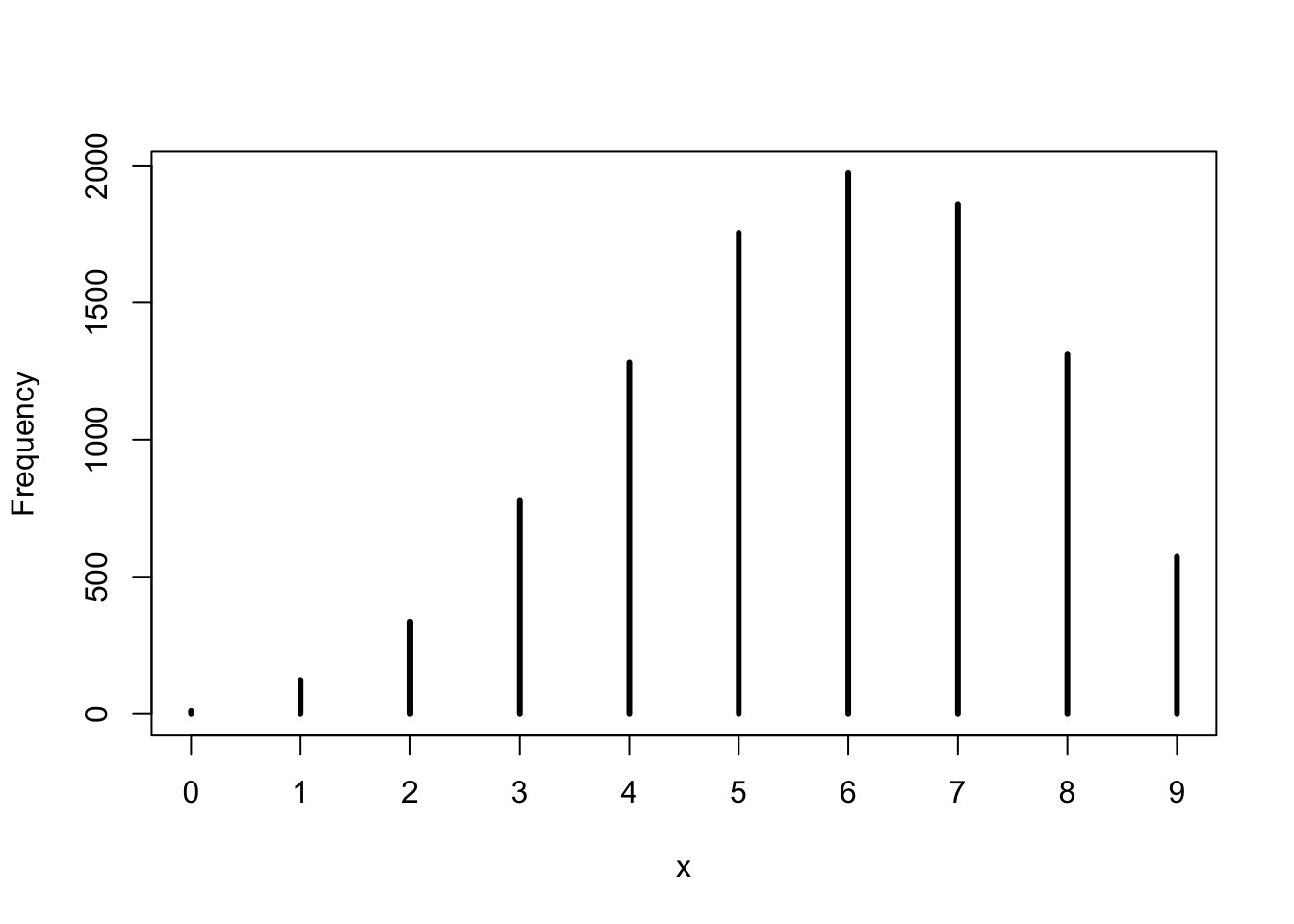
Note that 6 is the peak, and our draw was w=6!

Getting Fancier with Checking

  • We drew W,L,W,W,W,L,W,L,W

  • Can we reproduce 3 Ws as the longest run?

  • This will require fancier use of the posterior to simulate order of observations

  • See slide code - but, this empahsizes the subjective nature of model checking!

So, reproducing longest runs of W

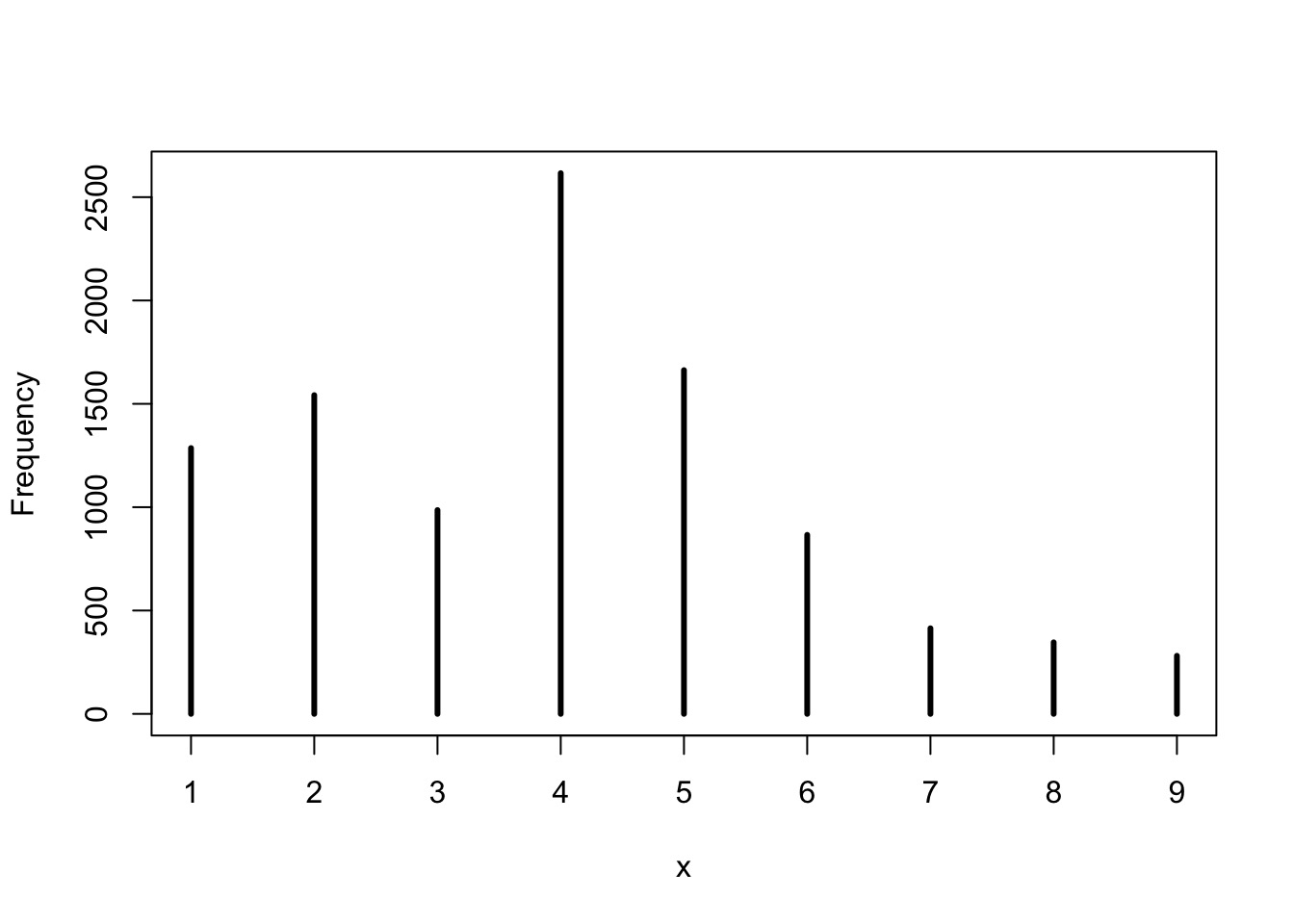
We had many 3s - not bad, not spot on - is this a good model or check?

Code

getRuns <- function(prob, draws=9){
  
  # toss that coin with a probability!
  toss <- rbinom(draws, size=1, prob)
  
  runs <- rle(toss) # gets run lengths of all values
  runs <- runs$length[runs$values == 1] # filter to 1
  
  # return 0 if all L, otherwise
  # return the longest
  if(length(runs) == 0){return(0)}
  max(runs)
}

# iterate over all samples
samp <- samp |>
  group_by(samp) |>
  mutate(longest_run = getRuns(samp)) |>
  ungroup()

simplehist(samp$longest_run)

Your Model is a Simlating Golem!

  • We can do a LOT with a simulated posterior

  • We can explore intervals and shape to create inferences

  • We can explore intervals and shape to validate our model

  • Using posteriors to generate random numbers means we can explore
    - If our model TRULY matches our data
    - Large-world relevance (external validity)
    - Future implications of our model

  • None of this is arbitrary statistical tests