Outline for Today

1. Who are you?

2. How will this course work?

3. What are we doing here?

4. Rethinking everything

Who are You?

1. Name

2. Lab

3. Brief research description

4. Why are you here?

Outline for Today

1. Who are you?

2. How will this course work?

3. What are we doing here?

4. Rethinking everything

Etherpads are Where it’s at!

https://etherpad.wikimedia.org/p/609-intro-2024

• To share polls and code

• Can use for collaborative note-taking

• Research shows that this enhances learning!

• It’s also a way to ask me a question during class

Second, Some Old Technology

• Green: Party on, Wayne
• Red: I fell off the understanding wagon
  
• Yellow: Slow down, Mister Teacher
  
• Blue: Write a question/Other

What Are We Covering?

How will this work?

Lectures are Coded

http://github.com/biol609/biol609.github.io

Interact via Slack

• Join the #Biol609 channel
  • https://umbrug.slack.com/
     

The Book: Statistical Rethinking 2nd Edition

## Some Scaffolding Reading

Before Every Class

The Questions I Will Ask About Readings at Random - What did you not get? (Don’t be shy!) (This might be all we talk about).

• What blew your mind?

• How do you apply this to your own work?

Final Paper

Do your research

(but be Bayesian about it)

Outline for Today

1. Who are you?

2. How will this course work?

3. What are we doing here?

4. Rethinking everything

Model-A-Palooza

Objective 1) To learn how to think about your study system and research question of interest in a systematic way and match it with a realistic process-based model.

Enter The Reverend

Objective 2) To understand how to build and fit complex models in a Bayesian framework.

The Rest of Your Life

Objective 3) Provide the grounding needed to effectively collaborate with statistical experts.

Objective 4) Allow students to gain the knowledge necessary to become life-long learners of data analysis techniques, able to incorporate new techniques into their analytic toolbelt as needed.

My True Goal in this Class

@juliaprogramming

Which one are you? #statistics #mathtok #mathematics #math #cs #computerscience #bayesian #stem #stemtok #probability #maths

♬ problems by mother mother - ₍ᵔ·͈༝·͈ᵔ₎

Outline for Today

1. Who are you?

2. How will this course work?

3. What are we doing here?

4. Rethinking everything

Outline for Today

1. Who are you?

2. How will this course work?

3. What are we doing here?

4. Rethinking everything

How do You View Data Analysis?

A Common Way to Think about Data Analysis

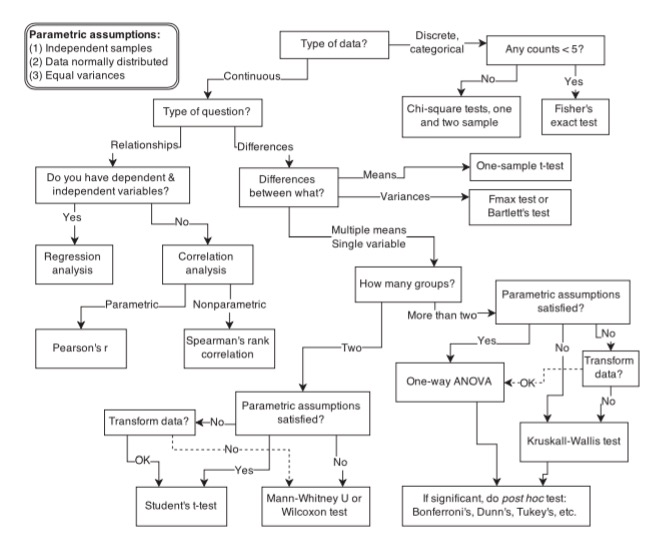
One Hypothesis ≠ One Statistical Model

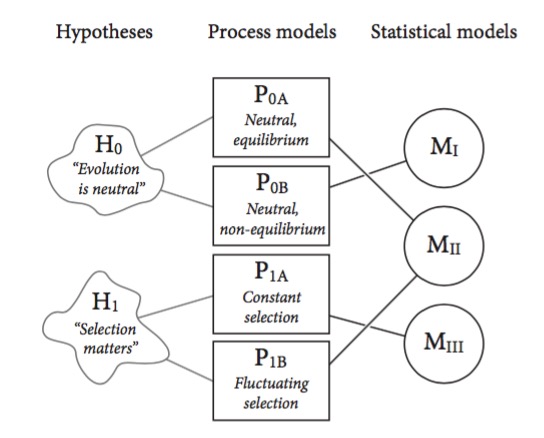
Back to Bayes-ics

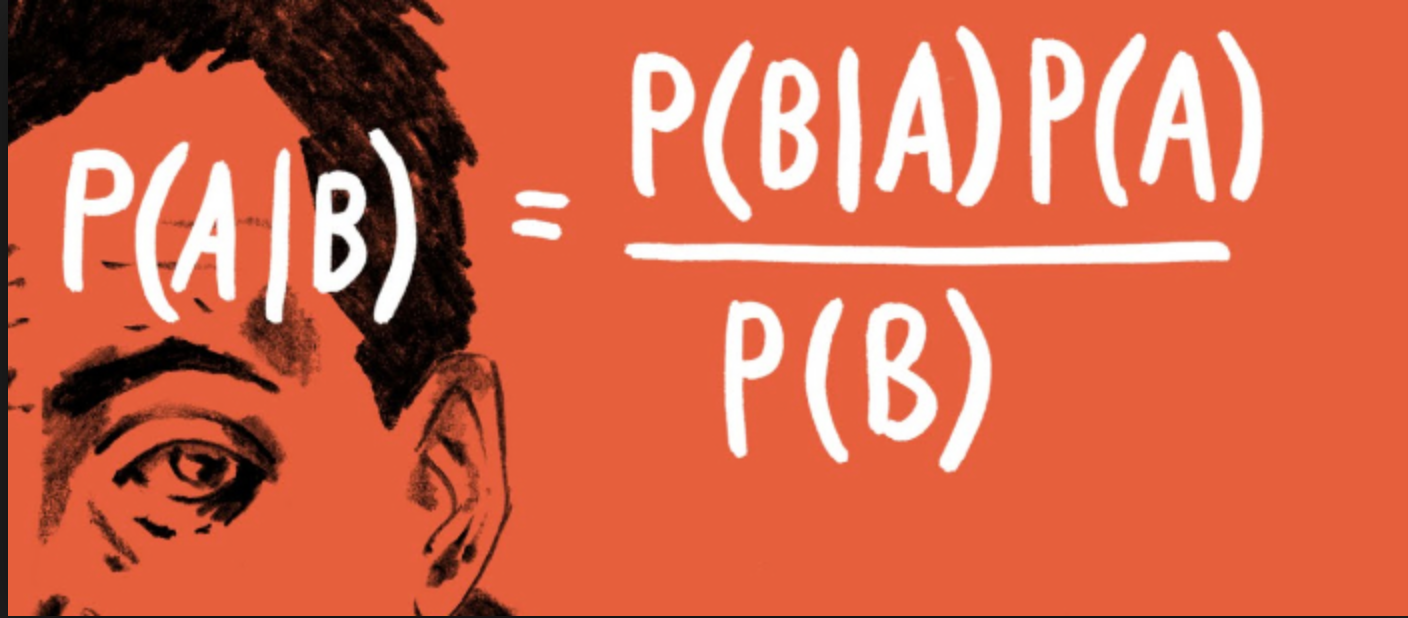
Bayesian Inference

• Frequentist: p(x ≤ D | H)
  
  
  
• Likelihood-ist: p( D | H)
  
  
  
• Bayesian: p(H | D)

Let’s see how Bayes works

I have a bag with 6 stones. Some are black. Some are white.

I’m going to draw stones, one at a time, with replacement, and let’s see the number of ways that the draw could have been produced.

After 4 draws, let’s calculate the probability of W white stones and B black stones. Let’s formalize how we made this calculation. This leads to conditional versus marginal probabilities.

Let’s see how Bayes works…

Now, I will look at the stones, and introduce a prior or some sort for W.

Let’s do a new set of draws, but this time, on the board, update our posterior.

And finally, relate this to the definition of Bayes theorem in 2.3.4 pg 36.

Let’s do this in R with Grid Sampling!

Use dplyr and mutate for the following.

0. Chose what fraction of stones is white in a bag of infinite size.
   
   
1. Creat a column of possible values from 0 to 1.
   
   
2. Define a prior as the second column.
   
   
3. Calculate your posterior after 1 random draw, then repeat for draws 2-4 plotting your posteriors
   • posterior = likelihood*prior/sum(all posterior values)
     
     
4. Plot your posterior given 100 draws, given your initial prior.

Introducing rethinking

This is from the Rcode on page 42, box 2.6. Assume 100 draws.

library(rethinking)

#alist is a list for used to define a model
draws_mod <- alist(
  
  #our likelihood
  w ~ dbinom(100, p)
  
  #our prior - can be something else if you want!
  p ~ dunif(0,1)
)

#define the data - you fill in the probability
draws_data <- list(w = XXX)

#We will use map - maximum a posteriori sampling
#Note, I use rethinking:: in case you've loaded purrr
draws_fit <- rethinking::map(draws_mod,
                             data = draws_data)

Now let’s explore our output

draws_fit

summary(draws_fit)